Лекции по автоматике 2Рефераты >> Радиоэлектроника >> Лекции по автоматике 2
Для систем выше второго порядка кроме положительности всех коэффициентов характеристического уравнения необходимо выполнение следующих неравенств:
1. Для систем третьего порядка 
2. Для систем четвертого порядка 
3. Для систем пятого порядка 
4. Для систем шестого порядка 
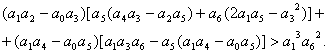
Пример. Дано характеристическое уравнение 
исследовать устойчивость системы по Гурвицу.
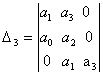
Для устойчивых систем необходимо 
и 
2. Критерий Рауса.
Критерий опубликован в 1877г.
Критерий Рауса используется при исследовании устойчивости систем высогкого порядка.
Формулировка критерия:
|
Для того чтобы вещественные части всех корней характеристического уравнения были отрицательны, необходимо и достаточно, чтобы все элементы первого столбца таблицы Рауса были отличны от нуля и имели один и тот же знак. |
Таблица Рауса.
|
|
|
|
| … |
|
|
|
|
| … |
|
|
|
|
| … |
|
|
|
|
| … |
|
|
|
|
|
Алгоритм заполнения таблицы: в первой и второй строках записываются коэффициенты уравнения с четными и нечетными индексами; элементы остальных строк вычисляются по следующему правилу: 
Достоинство критерия: можно исследовать устойчивость систем любого порядка.
Частотные критерии устойчивости.
Принцип аргумента.
В основе частотных методов лежит принцип аргумента (следствие теоремы Коши относительно числа нулей и полюсов аналитической функции).
Проведем анализ свойств многочлена вида:
где li - корни управления 
На комплексной плоскости каждому корню соответствует вполне определенная точка. Геометрически каждый корень li можно изобразить в виде вектора, проведенного из начала координат в точку li: |li| - длина вектора, argli - угол между вектором и положительным направлением оси абсцисс. Отобразим D(p) в пространство Фурье, тогда 
где jw-li - элементарный вектор.
Концы элементарных векторов находятся на мнимой оси.
- модуль вектор, а аргумент (фраза) 
Направление вращения вектора против часовой стрелки принимают за ПОЛОЖИТЕЛЬНОЕ. Тогда при изменении w от 
до 
каждый элементарный вектор (jw-li) повернется на угол +p, если li лежит в левой полуплоскости.
Пусть D(l)=0 имеет m корней в правой полуплоскости и n-m в левой, тогда при возрастании w до изменение аргумента вектора D(jw) (угол поворота D(jw), равный сумме изменений аргументов элементарных векторов) будет 
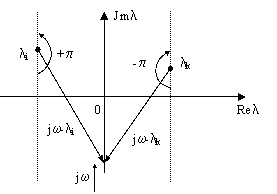
Принцип аргумента.
|
Изменение аргумента вектора D(jw) при возрастании w от |
Скачать реферат
