Лекции по автоматике 2Рефераты >> Радиоэлектроника >> Лекции по автоматике 2
За счёт внешнего воздействия – вынужденное движение.
Для ответа на вопрос, устойчива ли система или нет, надо решить однородное уравнение с начальными условиями.
Свободное колебание в системе определяются однородным дифференциальным уравнением ![]() решение которого имеет вид
решение которого имеет вид ![]() где
где
с1, с2…, сn- постоянные интегрирования, определяемые из начальных условий,
l1, l2…, ln – корни характеристического уравнения
![]()
Корни характеристического уравнения не зависят ни от вида возмущения, ни от начальных условий, а определяются только коэффициентами а0, а1, а2,…,аn, то есть параметрами и структурной системы.
| №№ п.п. | Корни характ. уравнения | Слагаемое Своб. решения | График функции члена реш. | Примечание | ||||
| 1 | 2 | 3 | 4 | 5 | ||||
|
| >0, действит. |
|
| |||||
|
| <0, действит. |
|
| Данный член®0 | ||||
|
| =0 |
| Система неустойчивая; возможно нейтральная | |||||
| Два нулевых корня |
|
| Система неустойчивая | ||||
|
| Корни комплексные, действительная часть положительная |
|
| Система неустойчивая | ||||
|
| Корни комплексные, действительная часть отрицательная |
|
| Возможно система устойчивая | ||||
|
| Корни мнимые сопряженные |
| Система неустойчивая; возможно на грани устойчивости |
Пояснения к таблице:
1. Если корни характеристического уравнения вещественные и неравные и среди корней имеется хотя бы один ПОЛОЖИТЕЛЬНЫЙ корень li, то соответствующее слагаемое ![]() - возрастающая экспонента, и весь процесс будет расходящимся.
- возрастающая экспонента, и весь процесс будет расходящимся.
2. Если характеристическое уравнение имеет пару мнимых сопряженных корней li = jw и li+1 = -jw, а остальные корни вещественные и отрицательные, то в этом случаев решении n-2 слагаемых - затухающие экспоненты вида ![]() , пара мнимых корней соответствуют два слагаемых
, пара мнимых корней соответствуют два слагаемых ![]() и
и ![]() . Пользуясь формулой Эйлера, напишем следующие равенства:
. Пользуясь формулой Эйлера, напишем следующие равенства:![]()
![]()
Следовательно, ![]()
Можно показать, сто Ci и Ci+1 - комплексно сопряженные числа, поэтому Ci + Ci+1 = A и j(Ci- Ci+1)=B являются вещественными числами.
Тогда ![]() где
где ![]()
![]() решение однородного дифференциального уравнения будет иметь вид
решение однородного дифференциального уравнения будет иметь вид ![]() - незатухающие и нерасходящиеся гармонические колебания.
- незатухающие и нерасходящиеся гармонические колебания.

 1
1  2
2 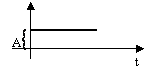 3
3 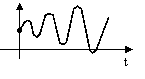 5
5  6
6 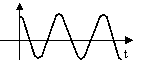 7
7