1.1.4 Теорема Пифагора

Тема: «Теорема Пифагора»

Цель: сформулировать и доказать теорему Пифагора.

В результате изучения данной темы учащиеся должны:

- знать формулировку теоремы Пифагора и ее доказательство;

- уметь применять полученные знания при решении задач.

Оборудование: чертежные и измерительные инструменты: линейка, транспортир, учебник для 7 – 11 кл, Погорелов, А.В. [20].

Фрагмент урока.

1. Актуализация опорных знаний.

Учитель предлагает ученикам вопросы и задания для выполнения, позволяющие вспомнить необходимые для усвоения нового материала факты.

- Что такое треугольник?

(Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.)

- Как называется треугольник, если у него все углы острые? (если один из углов тупой, прямой?)

(остроугольный, тупоугольный, прямоугольный)

2. Введение нового материала.

Учитель предлагает школьникам высказать предположения о справедливости следующей формулы: с2 = а2 + b2, где а и b – катеты прямоугольного треугольника, с – гипотенуза треугольника.

Ученикам выдаются модели прямоугольных треугольников.

Затем им предлагается провести измерения длин катетов прямоугольного треугольника и его гипотенузы и заполнить таблицу:

Таблица 6

Таким образом, ученики убедятся в истинности предположения, и уже после этого можно перейти к доказательству этого утверждения.

1.2 Использование измерений при решении задач

Еще одно направление использования измерений в геометрии, которое мы рассмотрим – это использование измерений при решении задач.

Часто решая какую-либо задачу, ученик сталкивается с рядом проблем: не знает с чего начать рассуждения, от чего отталкиваться и др. В таком случае может помочь непосредственное измерение. Школьник строит необходимый чертеж и измеряет элементы фигур, пытаясь найти какую-либо связь, зависимость между исходными данными и получаемыми результатами. Это помогает ученику найти способ решения задачи.

Пример 5. Дан треугольник АВС. Сторона АС равна 6 см. Высота, проведенная к АС, равна см см. Высота, проведенная к АВ, равна 3см. ÐС треугольника АВС равен 30°. Найти ÐА (рис. 38).

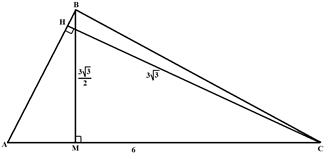
Рис. 38

При решении такой задачи дети могут не сразу догадаться, как же ее решить, им может потребоваться некоторая наводка. Они могут получить эту подсказку, если точно выполнят чертеж к задаче и найдут связь между исходными данными и неизвестными.

Дано:

∆АВС,

АС = 6 см,

ВМ = см – высота ∆АВС,

СН = 3см – высота ∆АВС,

ÐС = 30°,

Найти: ÐА.

Уже при построении чертежа от учеников требуется умение строить такие отрезки, как см. Это построение может быть выполнено следующим образом:

1. Сначала построим отрезок, равный см. Для этого построим прямоугольный треугольник с гипотенузой 2 см, а катетом 1 см. Тогда второй катет этого треугольника будет равен см (по теореме Пифагора) (рис. 39).

2. Затем мы три раза откладываем полученный отрезок и делим его пополам.

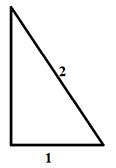
Рис. 39

Таким образом, при использовании такого вида измерения в качестве средства поиска решения задачи, учащиеся должны хорошо владеть измерительными и чертежными инструментами.

Построение (рис. 40):

1. АС = 6 см;

2. ÐС = 30°;

3.

4. ;

5. КР = ВМ, КÎ а;

6. b || АС, Р Î b;

7.

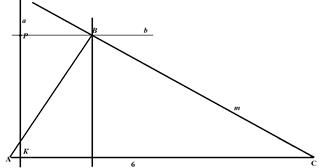
Рис. 40

После того, как школьник построил такой треугольник, он может измерить угол, который необходимо найти. Измерив ÐА, ученики убедятся, что он равен 60°, таким образом, треугольник АВС – прямоугольный. У школьников появятся мнения о том, с чего начать решение этой задачи – найти АВ, после чего, показать, что треугольник, в самом деле, прямоугольный.

А уже после того, как ребенок нашел способ решения этой задачи, он ее решает с использованием косвенных измерений.

(Решение:

1. Найдем площадь треугольника АВС:

С одной стороны: (см2);

С другой стороны: . Откуда АВ = (см)

2. ÐС = 30°, АС = 6 см, АВ = 3 см, сл-но, ∆АВС – прямоугольный, ÐВ = 90°, ÐА = 60°.

Ответ: ÐА = 60°.)

Непосредственные и косвенные измерения также могут помочь в решении задач.

Пример 6. Дана монета (монета имеет форму окружности) (рис. 41). Найти ее радиус.

Рис. 41

Ученики с помощью нити измеряют длину окружности, а затем вычисляют ее радиус по уже известной им формуле.

Заметим, что использование информационных измерений при решении задач возможно, но в большинстве случаев они помогают лишь вычислить что-то, не позволяют ученику понять ход решения. Использование информационных измерений при решении задач оказывают влияние в следующих случаях:

- для четкого построения чертежа. С помощью компьютерных технологий школьник может сделать правильный и точный чертеж к задаче, а после этого перейти к поиску решений.

- Решение задач на ГМТ.

- Решение задач исследовательского характера.

Пример 7. Дан равносторонний треугольник со стороной а и окружность с радиусом, равным стороне треугольника. Определить, сколько возможно точек пересечения окружности со сторонами треугольника.