Движение в центрально-симметричном поле
Содержание:
1. Движение в центрально-симметричном поле.
2. Падение частицы на центр.
3. Движение в кулоновом поле ( сферические координаты ).
1.Движение в центрально-симметричном поле.
Задача о движении двух взаимодействующих друг с другом частиц в квантовой механике может быть сведена к задаче об одной частице, - аналогично тому, как это может быть сделано в классической механике. Гамильтониан двух частиц ( с массами 
) , взаимодействующих по закону 
-расстояние между частицами), имеет вид
(1,1)
где 
- операторы Лапласа по координатам частиц. Введем вместо радиусов-векторов частиц 
и 
новые переменные 
и 
:
(1,2)
- вектор взаимного расстояния, а - радиус-вектор центра инерции частиц. Простое вычисление приводит к результату:
(1,3)
( 
и 
- операторы Лапласа соответственно по компонентам векторов и ;
- полная масса системы; 
- приведенная масса). Таким образом, гамильтониан распадается на сумму двух независимых частей. Соответственно этому, можно искать 
в виде произведения 
, где функция 
описывает движение центра инерции ( как свободное движение частицы с массой ), а 
описывает относительное движение частиц ( как движение частицы массы 
в центрально-симметричном поле 
).
Уравнение Шредингера для движения частицы в центрально-симметричном поле имеет вид
(1,4)
Воспользовавшись известным выражением для оператора Лапласа в сферических координатах, напишем это уравнение в виде
.
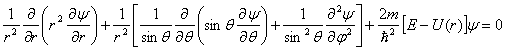(1,5)
Если ввести сюда оператор квадрата момента:
,
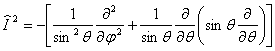то мы получим
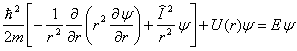(1,6)
При движении в центрально-симметричном поле момент импульса сохраняется. Будем рассматривать стационарные состояния с определенными значениями момента 
и его проекции . Заданием значений и определяется угловая зависимость волновых функций. Соответственно этому, ищем решения уравнения (1,6) в виде
(1,7)
где 
- сферические функции. Поскольку 
, то для «радиальной функции» 
получаем уравнение
(1,8)
Это уравнение не содержит вовсе значения 
, что соответствует 
-кратному вырождению уровней по направлениям момента.
Займемся исследованием радиальной части волновых функций. Подстановкой
(1,9)
уравнение (1,8) приводится к виду
(1,10)
Если потенциальная энергия везде конечна, то должна быть конечной во всем пространстве, включая начало координат, также и волновая функция 
, а следовательно, и ее радиальная часть . Отсюда следует, что 
должна обращаться в нуль при 
:
(1,11)
В действительности это условие сохраняется также и для поля, обращающегося при 
в бесконечность.
Уравнение (1,10) по форме совпадает с уравнением Шредингера для одномерного движения в поле с потенциальной энергией
(1,12)
равной сумме энергии , и члена
,
который можно назвать центробежной энергией. Таким образом, задача о движении в центрально-симметричном поле сводится к задаче об одномерном движении в области, ограниченной с одной стороны ( граничное условие при ). «Одномерный характер» имеет также и условие нормировки для функции 
, определяющееся интегралом
.
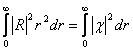При одномерном движении в ограниченной с одной стороны области уровни энергии не вырождены. Поэтому можно сказать, что заданием значения энергии решение уравнения (1,10), т.е. радиальная часть волновой функции, определяется полностью. Имея также в виду, что угловая часть волновой функции полностью определяется значениями и , мы приходим к выводу, что при движении в центрально-симметричном поле волновая функция полностью определяется значениями 
. Другими словами, энергия, квадрат момента и его проекция составляют полный набор физических величин для такого движения.
Скачать реферат
