Движение в центрально-симметричном поле

Рефераты >> Физика >> Движение в центрально-симметричном поле

с двумя корнями

, (2,3)

Для дальнейшего исследования удобно поступить следующим образом. Выделим вокруг начала координат малую область радиуса и заменим функцию в этой области постоянной величиной . Определив волновые функции в таком «обрезанном» поле, мы затем посмотрим, что получается при переходе к пределу .

Предположим сначала, что . Тогда и - вещественные отрицательные числа, причем >. При общее решение уравнения Шредингера имеет вид ( везде речь идет о малых )

(2,4)

(- постоянные). При решение уравнения

конечное в начале координат, имеет вид

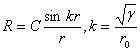(2,5)

При функция и ее производная должны быть непрерывными функциями. Удобно написать одно из условий в виде условия непрерывности логарифмической производной от . Это приводит к уравнению

или

.

Решенное относительно , это уравнение дает выражение вида

(2,6)

Переходя теперь к пределу , находим, что ( напоминаем, что ). Таким образом, из двух расходящихся в начале координат решений уравнения Шредингера (2,1) должно быть выбрано то, которое обращается в бесконечность менее быстро:

.

Пусть теперь . Тогда и комплексны:

.

Повторяя предыдущие рассуждения, снова придем к равенству (2,6), которое при подстановке значений и дает

. (2,8)

При это выражение не стремится ни к какому определенному пределу. Так что прямой переход к пределу невозможен. С учетом (2,8) общий вид вещественного решения может быть написан следующим образом:

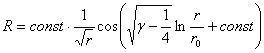. (2,9)

Эта функция обладает нулями, число которых неограниченно растет с уменьшением . Поскольку, с одной стороны, выражение (2,9) справедливо для волновой функции ( при достаточно малых ) при любом конечном значении энергии частицы, а, с другой стороны, волновая функция нормального состояния совсем не должна иметь нулей, то мы можем заключить, что «нормальное состояние2 частицы в рассматриваемом поле соответствует энергии . Но во всяком состоянии дискретного спектра частица находится в основном в области пространства, в которой . Поэтому при частица находится в бесконечно малой области вокруг начала координат, т.е. происходит «падение» частицы в центр.

«Критическое» поле , при котором становится возможным падение частицы в центр, соответствует значению . Наименьшее значение коэффициента при получается при , т.е.

. (2,10)

Из формулы (2,8) ( для ) видно, что допускаемое решение уравнения Шредингера ( вблизи точки, где ) расходится при не быстрее чем . Если поле обращается при в бесконечность медленнее чем , то в уравнении Шредингера в области вблизи начала координат можно вовсе пренебречь по сравнению с остальными членами, и мы получим те же решения, что и для свободного движения, т.е. . Наконец, если поле обращается в бесконечность быстрее чем ( как с ), то волновая функция вблизи начала координат пропорциональна . Во всех этих случаях произведение обращается при в нуль.