Вспоминая определение (3,3) параметра , находим

(3,9)

Этим решается задача об определении уровнем энергии дискретного спектра в кулоновском поле. Мы видим, что имеется бесконечное множество уровней между нормальным уровнем и нулем. Интервалы между каждыми двумя последовательными уровнями уменьшаются с увеличением ; уровни сгущаются по мере приближения к значению , при котором дискретный спектр смыкается с непрерывным. В обычных единицах формула (3,9) имеет следующий вид:

(3,10)

Целое число называется главным квантовым числом. Радиальное же квантовое число, определенное в п.1, равно

.

При заданном значении главного квантового числа число может принимать значения

(3,11)

всего различных значений. В выражение (3,9) для энергии входит только число . Поэтому все состояния с различными , но одинаковыми обладают одинаковой энергией. Таким образом, каждое собственное значение оказывается вырожденным не только по магнитному квантовому числу ( как при всяком движении в центрально-симметричном поле ), но и по числу . Это последнее вырождение ( о нем говорят, как о случайном или кулоновом ) специфично именно для кулонового поля. Каждому данному значению соответствует различных значений ; поэтому кратность вырождения - го уровня энергии равна

(3,12)

Волновые функции стационарных состояний определяются формулами (3,5), (3,7). Вырожденная гипергеометрическая функция с целыми значениями обоих параметров совпадает, с точностью до множителя, с так называемыми обобщенными полиномами Лагерра. Поэтому

.

Радиальные функции должны быть нормированы условием

.

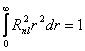Их окончательный вид следующий:

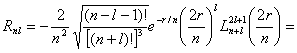
(3,13)

Вблизи начала координат имеет вид

(3,14)

На больших расстояниях

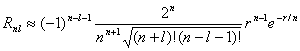. (3,15)

Волновая функция нормального состояния затухает экспоненциально на расстояниях порядка , т.е. в обычных единицах, .

Средние значения различных степеней вычисляются по формуле

.

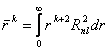Приведем несколько первых величин ( с положительными и отрицательными ):

, ,

, . (3,16)

Непрерывный спектр.

Спектр положительных собственных значений непрерывен и простирается от нуля до бесконечности. Каждое из этих собственных значений вырождено с бесконечной кратностью; каждому значению соответствует бесконечное множество состояний с , пробегающими все целые значения от до ( и со всеми возможными, при данных , значениями ).

Определяемое формулами (3,3) число и переменная теперь чисто мнимы:

, , (3,17)

где . Радиальные собственные функции непрерывного спектра имеют вид

(3,18)

где - нормировочный множитель. Они могут быть представлены в виде комплексного интеграла

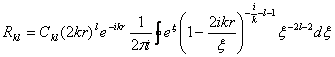, (3,19)

который берется по контуру ( см. рис ниже ).

Подстановкой этот интеграл приводится к более симметричному виду

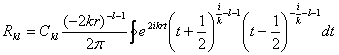(3,20)

( путь интегрирования обходит в положительном направлении точки ). Из этого выражения непосредственно видно, что функции вещественны.