в стационарном режиме удовлетворяет системе уравнений

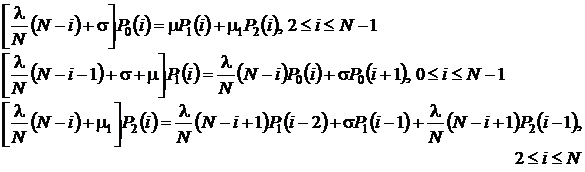(4.1)

4.1. Асимптотический анализ распределения вероятностей состояний сети

Систему уравнений (4.1) будем решать асимптотическим методом марковизируемых систем [7] при .

Первое приближение

В системе уравнений (4.1) сделаем следующие замены переменных: . В результате такой замены производится переход от дискретной переменной к непрерывной переменной . В новых обозначениях система (4.1) примет вид

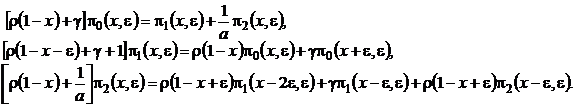(4.2)

Получим вид решения системы (4.2), которую будем решать в два этапа.

1 этап. Устремим к нулю и обозначим . Тогда система (4.2) перейдет в систему

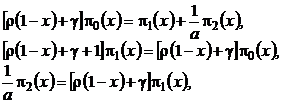(4.3)

решение которой имеет вид

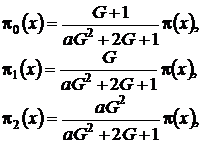(4.4)

где 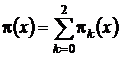– асимптотическая плотность распределения вероятностей нормированного числа заявок в ИПВ.

Осталось найти вид функции , для этого перейдем ко второму этапу.

2 этап. В системе (4.2) все функции с аргументом разложим в ряд по приращению аргумента , ограничиваясь слагаемыми порядка , получим

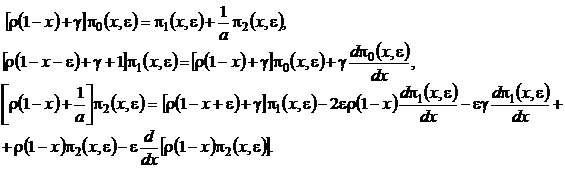(4.5)

Сложив все уравнения системы, будем иметь

(4.6)

В полученном равенстве поделим левую и правую части на и , прейдем к такому равенству

(4.7)

Подставим в (4.7) функции в форме (4.4) и получим

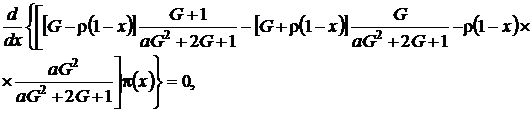(4.8)

следовательно

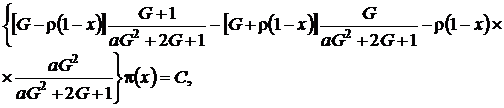(4.9)

где С – некоторая постоянная.

Необходимо найти константу C. Нетрудно заметить, что при х=0 выражение в фигурных скобках не положительно, следовательно , а при х=1 . Итак, . Таким образом, произведение двух функций равно нулю, следовательно, может принимать какое-либо ненулевое значение лишь в тех точках, в которых выражение в скобках равно нулю.

Получим функцию , везде равную нулю, за исключением точек, являющихся корнями уравнения

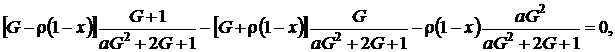
после преобразований это выражение принимает вид

(4.10)

Так как – плотность распределения вероятностей, то должно выполняться условие нормировки 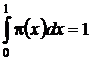. Этим условиям удовлетворяет лишь функция вида

,

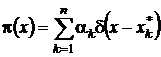где – корни уравнения (4.10), n – число корней, .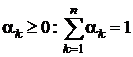

Если уравнение (4.10) имеет единственный корень , то эту точку назовем точкой стабилизации, потому что она является модой распределения вероятностей нормированного процесса заявок в ИПВ , и в ее окрестности достаточно долго флуктуируют значения этого процесса. В этом случае назовем сеть моностабильной.

Второе приближение

Пусть уравнение (4.10) имеет единственный корень , то есть плотность распределения исследуемой сети сосредоточена около точки . Найдем плотность распределения отклонения от этой точки. Для этого в системе (4.1) сделаем замену переменных:, , .

В новых обозначениях система (4.1) примет вид

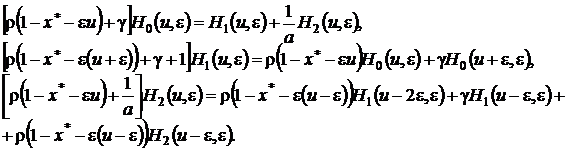(4.11)

Систему (4.11) будем решать в три этапа.

1 этап. Устремим к нулю и обозначим , тогда система (4.11) перейдет в систему

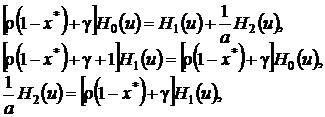(4.12)

решение которой имеет вид

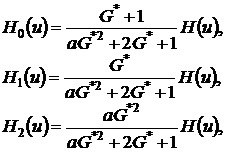(4.13)

где , 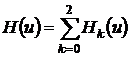– плотность распределения нормированной величины отклонения процесса от значения – корня уравнения (4.10).

Найдем вид функции .

2 этап. Неизвестные функции будем искать в форме

(4.14)

где 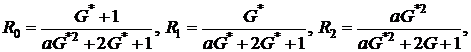(4.15)

– асимптотическая вероятность того, что состояние обслуживающего канала равно .