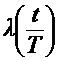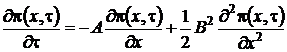, (1.17)

где

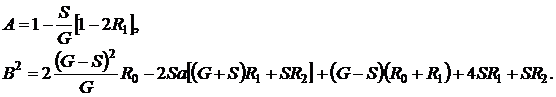
Решим уравнение (1.17) с помощью преобразования Лапласа по x. Левую и правую части уравнения умножим на и проинтегрируем. С учетом обозначения 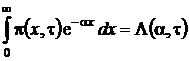и свойств этой функции уравнение (1.17) приобретет вид

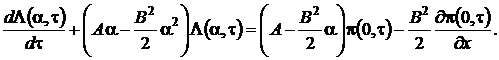(1.18)

Таким образом, мы перешли от уравнения Фоккера-Планка с постоянными коэффициентами к обыкновенному дифференциальному уравнению, решение которого с точностью до неизвестных , и записывается следующим образом

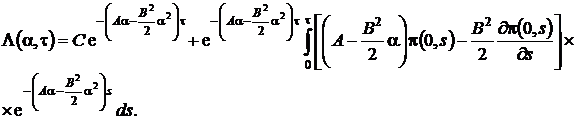(1.19)

Для того чтобы получить окончательное решение уравнения (1.17) нужно провести дополнительное исследование, которое бы показало поведение исследуемого процесса в окрестности нуля. Используя асимптотику , это не удается сделать.

Предположим, что сеть связи функционирует в стационарном режиме, тогда (1.17) перепишется в виде

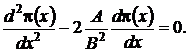(1.20)

Следовательно, в стационарном режиме асимптотическое распределение вероятностей нормированного числа заявок в источнике повторных вызовов подчиняется экспоненциальному закону с параметром и имеет вид

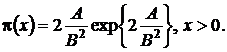(1.21)

2. Исследование неоднородной нестационарной сети случайного доступа с динамическим протоколом в условиях перегрузки

Рассмотрим сеть связи, описанную в разделе 1, в которой интенсивность входящего потока зависит от времени и равна , где Т – некоторый интервал времени, в течение которого функционирует сеть связи. Структура сети изображена на рис. 2.1.

Рис. 2.1 – Модель системы массового обслуживания

В нестационарном режиме распределение

удовлетворяют системе дифференциально-разностных уравнений вида

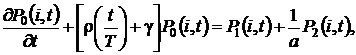
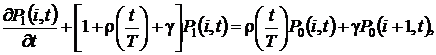(2.1)

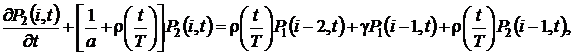
где , , , .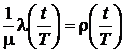

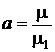Замечание: система уравнений (2.1) получена аналогично системе уравнений (1.1). Вероятности переходов для состояний системы совпадают с точностью до замены .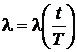

Систему (2.1) будем решать в условиях перегрузки, то есть при .

Первое приближение

В системе уравнений (2.1) произведем замену переменных: . В результате такой замены производится переход от дискретной переменной к непрерывной переменной , от t перешли к , причем такое, что . После замены производная равна .

Тогда уравнения (2.1) перепишем

(2.2)

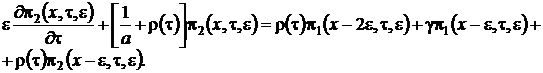
Решим систему уравнений (2.2) в два этапа.

1 этап. Считая и предполагая, что будем иметь

(2.3)

.

Выразим через функцию 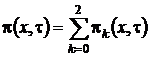и получим