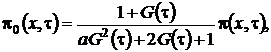
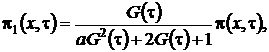(2.4)

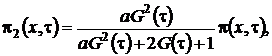
где асимптотическая плотность распределения нормированного числа заявок в источнике повторных вызовов.

Обозначим

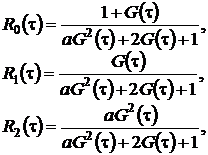(2.5)

( - это асимптотическая вероятность того, что обслуживающий прибор находится в состоянии k). Заметим, что из системы (2.3) следуют равенства связывающие , и

(2.6)

.

Найдем вид функции , для этого перейдем ко второму этапу.

2 этап. В системе дифференциальных уравнений (2.2) все функции с аргументом разложим в ряд по приращению аргумента , ограничиваясь слагаемыми порядка , получим

(2.7)

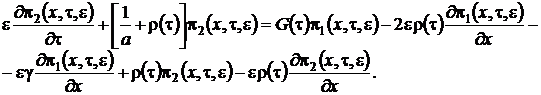
Просуммируем левые и правые части уравнений системы (2.7) и получим равенство

. (2.8)

С учетом того, что

равенство (2.8) принимает вид

. (2.9)

Уравнение (2.9) является однородным линейным уравнением с частными производными первого порядка. Для того чтобы его решить составим уравнение

,

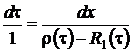его решение , тогда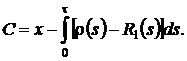

Общее решение уравнения (2.9) имеет вид

, (2.10)

где - произвольная дифференцируемая функция, аналитическое выражение которой найдем из начальных условий.

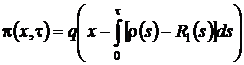Пусть распределение в начальный момент времени где некоторая плотность распределения. Тогда следовательно . Возьмем в качестве начальной плотности распределения , где - дельта-функция Дирака, а , - число заявок в источнике повторных вызовов в начальный момент времени.

Таким образом , из свойств функции Дирака следует, что .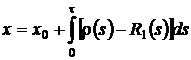

То есть мы получили, что , имеет смысл асимптотического среднего.

Из приведенных рассуждений вытекает еще одно важное следствие, а именно

имеет место , тогда (отрицательная функция противоречит смыслу задачи). В нашем случае совпадает с пропускной способностью системы.

Перейдем ко второму приближению, в котором будем искать распределение отклонения от асимптотического среднего.

Второе приближение

В исходной системе уравнений (2.1) сделаем замену переменных .

Заметим, что в новых обозначениях производная по времени равна 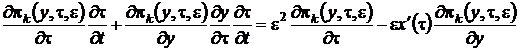. С учетом этого система (2.1) примет вид

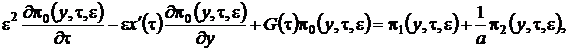
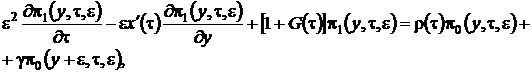(2.11)

Решение системы уравнений (2.11) аналогично решению системы (2.2), но проводится в три этапа.

1 этап. В системе дифференциальных уравнений (2.13) сделаем предельный переход при и предположим, что , получим

(2.12)

.

Решим эту систему аналогично тому, как решили систему уравнений (2.3). Введем функцию 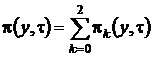и выразим через нее , получим

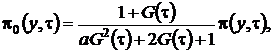
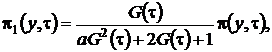(2.13)

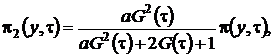
где асимптотическая плотность распределения отклонения числа заявок в источнике повторных вызовов от асимптотического среднего.

2 этап. Функции будем искать с точностью до в форме

(2.14)

Найдем вид функций , и . Для этого в системе дифференциальных уравнений (2.11) все функции с аргументом разложим в ряд по приращению аргумента , ограничимся слагаемыми порядка . Получим