Морфологический анализ цветных (спектрозональных) изображений

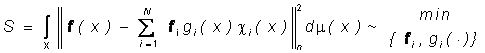(18)

Речь идет о задаче аппроксимации произвольного изображения изображениями, у которых яркость может быть произвольной функцией из , в то время, как цвет должен сохранять постоянное значение на каждом из заданных подмножеств A1, .,AN поля зрения X, (см. Лемму 3).

Так как

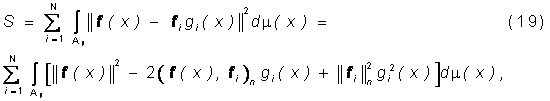
то минимум S (19) по достигается при

, (20)

и равен

(21)

Задача (18) тем самым сведена к задаче

. (22)

В связи с последней рассмотрим самосопряженный неотрицательно определенный оператор

. (23)

Максимум (неотрицательной) квадратичной формы на сфере в Rn, как известно, (см.,например, [11]) достигается на собственном векторе yi оператора Фi, отвечающем максимальному собственному значению >0,

,

и равен , т.е. . Следовательно, максимум в (22) равен и достигается, например, при

Теорема 3. Пусть A1, .,AN -заданное измеримое разбиение X, причем[9] m(Ai)>0, i=1, .,N. Решением задачи (18) наилучшего приближения изображения изображениями g(×) (17) является изображение

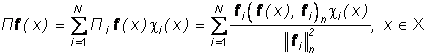(24)

Операторы ,i=1, .,N, и - нелинейные (зависящие от f(×)) проекторы: Пi проецирует в Rn векторы на линейное подпространство , натянутое на собственный вектор оператора Фi (23), отвечающий наибольшему собственному значению ri,

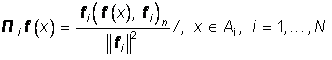; (25)

П проецирует в изображение на минимальное линейное подпространство , содержащее все изображения

Невязка наилучшего приближения

(19*).

Доказательство. Равентство (24) и выражение для Пi следует из (17),(20) и решения задачи на собственные значения для оператора Фi (23). Поскольку Фi самосопряженный неотрицательно определенный оператор, то задача на собственные значения (23) разрешима, все собственные значения Фi неотрицательны и среди них ri - наибольшее.

Для доказательства свойств операторов Пi, i=1, .,N, и П введем обозначения, указывающие на зависимость от f(×):

(26*)

Эти равенства, показывающие, что результат двукратного действия операторов Пi, i=1, .,N, и П (26) не отличается от результатата однократного их действия, позволят считать операторы (26) проекторами.

Пусть fi - cсобственный вектор Фi , отвечающий максимальному собственному значению ri. Чтобы определить следует решить задачу на собственные значения для оператора :

.

Поскольку rank=1, имеет единственное положительное собственное значение, которое, как нетрудно проверить, равно ri, и ему соответствует единственный собственный вектор fi. Поэтому

.

Отсюда, в свою очередь, следует равенство (26*) для n

Лемма 4. Для любого изображения решение (24) задачи (18) наилучшего приближения единственно и является элементом .

Доказательство. Достаточно доказать, что единственный (с точностью до положительного множителя) собственный вектор fi оператора (23), отвечающий максимальному собственному значению ri, можно выбрать так, чтобы , поскольку в таком случае будут выполнены импликации:

,

составляющие содержание леммы. Действительно, если то согласно (23) , поскольку включение означает, что; отсюда и из (25) получим, что ,i=1, .,N, а поэтому и в (24) .

Страница:

Последние рефераты