Морфологический анализ цветных (спектрозональных) изображений

где , и имеет мало общего с разбиением (14).

Замечание 3. Выберем векторы fi, i=1, ,q единичной длины: , i=1, .,q. Тогда

. (16)

Множества (16) являются конусами в Rn , ограниченными гиперплоскостями, проходящими через начало координат. Отсюда следует, что соответствующее приближение изображения f(×) инвариантно относительно произвольного преобразования последнего, не изменяющего его цвет (например ), в частности, относительно образования теней на f(×).

Замечание 4. Для любого заданного набора попарно различных векторов оператор F, приведенный в теореме 2, определяет форму изображения, принимающего значения соответственно на измеримых множествах (любого) разбиения X. Всякое такое изображение является неподвижной (в ) точкой F: , если , все они изоморфны между собой. Если некоторые множества из - пустые, или нулевой меры, соответствующие изображения имеют более простую форму.

Иначе говоря, в данном случае формой изображения является множество всех изображений, принимающих заданные значения на множествах положительной меры любого разбиения X, и их пределов в .

Теоремы 1 и 2 позволяют записать необходимые и достаточные условия наилучшего приближения изображения f(×) изображениями , в котором требуется определить как векторы , так и множества так, чтобы

.

Следствие 1.

Пусть Di ,i=1, .,N, - подмножества Rn (15), П - ортогональный проектор (13), , где . Тогда необходимые и достаточные условия суть следующие: , где , .

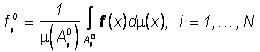Следующая рекуррентная процедура, полезная для уточнения приближений, получаемых в теоремах 1,2, в некоторых случаях позволяет решать названную задачу. Пусть - исходные векторы в задаче (14*), - соответствующее оптимальное разбиение (14), F(1)- оператор наилучшего приближения и - невязка. Воспользовавшись теоремой 1, определим для найденного разбиения оптимальные векторы . Согласно выражению (13) 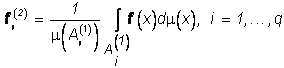, и соответствующий оператор наилучшего приближения П(1) (13) обеспечит не менее точное приближение f(×), чем F(1): . Выберем теперь в теореме 2 , определим соответствующее оптимальное разбиение и построим оператор наилучшего приближения F(2). Тогда . На следующем шаге по разбиению строим и оператор П(3) и т.д.

В заключение этого пункта вернемся к вопросу о построении исчерпывающего -измеримого разбиения X, отвечающего заданной функции . Выберем произвольно попарно различные векторы из f(X) и построим по формуле (15) разбиение Rn . Для каждого q=1,2, . образуем разбиение E(N(q)), множества , j=1, .,N(q), которого образованы всеми попарно различными пересечениями множеств из . Последовательность соответствующих разбиений X , i=1, .,N(q), q=1,2 . -измеримы и является продолжением

5.2. Приближение изображениями, цвет которых постоянен на подмножествах разбиения поля зрения X.

Задано разбиение , требуется определить цвет и распределение яркостей наилучшего приближения на каждом Ai,i=1, .,N.

Для практики, как уже было отмечено, большой интерес представляет класс изображений (5), цвет которых не изменяется в пределах некоторых подмножеств поля зрения, и задачи аппроксимации произвольных изображений изображениями такого класса.

Запишем изображение (5) в виде

(17)

где .

Пусть A1, .,AN - заданное разбиение X, - индикаторная функция Ai, i=1, .,N. Рассмотрим задачу наилучшего в приближения изображения изображениями (17), не требуя, чтобы

Страница:

Последние рефераты