Морфологический анализ цветных (спектрозональных) изображений

где - класс преобразований , такой, что . Иначе можно считать, что

(10*)

а - оператор наилучшего приближения элементами множества , форма которых не сложнее, чем форма . Характеристическим для является тот факт, что, если f(x)=f(y), то для любого .

5.1. Приближение цветного изображения изображениями, цвет и яркость которых постоянны на подмножествах разбиения поля зрения X.

Задано разбиение , требуется определить яркость и цвет наилучшего приближения на каждом . Рассмотрим задачу наилучшего приближения в цветного изображения f(×) (2) изображениями (4), в которых считается заданным разбиение поля зрения X и требуется определить из условия

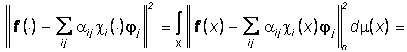
(11)

Теорема 1. Пусть . Тогда решение задачи (11) имеет вид

, i=1, .,N, j=1, .,n, (12)

и искомое изображение (4) задается равенством

. (13)

Оператор является ортогональным проектором на линейное подпространство (4****) изображений (4), яркости и цвета которых не изменяются в пределах каждого Ai , i=1, .,N.

Черно-белый вариант (4*) цветного изображения (4) является наилучшей в аппроксимацией черно-белого варианта цветного изображения f(×) (2), если цветное изображение (4) является наилучшей в аппроксимацией цветного изображения f(×) (2). Оператор 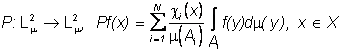, является ортогональным проектором на линейное подпространство черно-белых изображений, яркость которых постоянна в пределах каждого .

В точках множества цвет 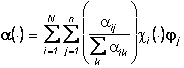(4**) наилучшей аппроксимации (4) цветного изображения f(×) (2) является цветом аддитивной смеси составляющих f(×) излучений, которые попадают на .

Доказательство. Равенства (12) - условия минимума положительно определенной квадратичной формы (11), П - ортогональный проектор, поскольку в задаче (11) наилучшая аппроксимация - ортогональная проекция f(×) на . Второе утверждение следует из равенства

, вытекающего из (13). Последнее утверждение следует из равенств

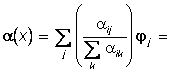
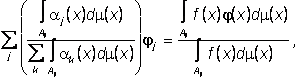
,i=1, .,N вытекающих из (12) и равенства (1), в котором индекс k следует заменить на xÎX. ■

Замечание 1. Для любого измеримого разбиения ортогональные проекторы и определяют соответственно форму в широком смысле цветного изображения (4), цвет и яркость которого, постоянные в пределах каждого , различны для различных , ибо , и форму в широком смысле черно-белого изображения, яркость которого постоянна на каждом и различна для разных ,[2].

Если учесть, условие физичности (2*), то формой цветного изображения следует считать проектор на выпуклый замкнутый конус (4***)

Аналогично формой черно-белого изображения следует считать проектор на выпуклый замкнутый конус изображений (4*), таких, что [2]. Дело в том, что оператор определяет формуизображения (4), а именно

- множество собственных функций оператора . Поскольку f(×) - наилучшее приближение изображения изображениями из , для любого изображения из и только для таких - . Поэтому проектор можно отождествить с формой изображения (4).

Страница:

Последние рефераты