Морфологический анализ цветных (спектрозональных) изображений

4. Форма кусочно-постоянного (мозаичного) цветного изображения.

Во многих практически важных задачах форма объекта на изображении может быть охарактеризована специальной структурой излучения, достигающего поле зрения X в виде здесь - индикаторные функции непересекающихся подмножеств Аi, i=1,… .,N, положительной меры поля зрения Х, на каждом из которых функции 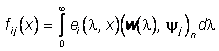, , j=1, .,n, i=1, .,N, непрерывны. Поскольку согласно лемме 2

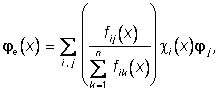
, (3)

то цветное изображение fe(×), такого объекта характеризует его форму непрерывным распределением яркости и цвета на каждом подмножестве Ai, i=1, .,N. Для изображения , где , также характерно напрерывное распределение яркости и цвета на каждом Ai, если , - непрерывные функции.

Если, в частности, цвет и яркость постоянны на Ai, i=1, .,N, то это верно и для всякого изображения , если не зависит явно от . Для такого изображения примем следующее представление:

, (4)

его черно-белый вариант

(4*)

на каждом Ai имеет постоянную яркость , и цвет изображения 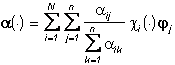(4)

(4**)

не меняется на Ai и равен 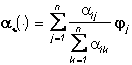, i=1, .,N.

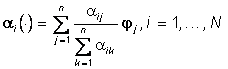Поскольку для реальных изображений должно быть выполнено условие физичности (2*), , то форму изображения (4), имеющего на различных множествах Аi имеет несовпадающие яркости и различные цвета , определим как выпуклый замкнутый в конус:

. (4***)

v(a), очевидно, содержится в n×N мерном линейном подпространстве

, (4****)

которое назовем формой a(×) в широком смысле.

Форму в широком смысле любого изображения a(×), у которого не обязательно различны яркости и цвета на различных подмножествах Ai ,i=1, .,N, определим как линейное подпространство , натянутое не вектор-функции Fa(×),FÎF, где F - класс преобразований , определенных как преобразования векторов a(x)®Fa(x) во всех точках xÎX; здесь F - любое преобразование . Тот факт, что F означает как преобразование , так и преобразование , не должен вызывать недоразумения.

Изображения из конуса(4***) имеют форму, которая не сложнее, чем форма a(×) (4), поскольку некоторые из них могут иметь одно и то же значение яркости или(и) цвета на различных множествах Аi, i=1,………… ,N. Также множества оказываются, по существу, объединенными в одно, что и приводит к упрощению формы изображения, поскольку оно отражает меньше деталей формы изображенного объекта, чем изображение (4). Это замечание касается и L(a(×)), если речь идет о форме в широком смысле.

Лемма 3. Пусть {Аi} - измеримое разбиение X: .

Изображение (3) имеет на каждом подмножестве Ai :

- постоянную яркость и цвет , если и только если выполняется равенство (4);

- постоянный цвет , если и только если в (3) ;

- постоянную яркость fi , i=1, .,N, если и только если в (3) не зависит от , i=1,… .,N.

Доказательство . На множестве Ai яркость и цвет изображения (3) равны соответственно[6]

, , i=1,.… ,N.

Если выполнено равенство (4), то и от не зависят. Наоборот, если и , то и , т.е. выполняется (4).

Если , то цвет не зависит от . Наоборот, пусть не зависит от . В силу линейной независимости координаты j(i)(x) не зависят от , т.е. и, следовательно, где - яркость на A i и . Последнее утверждение очевидно n

Страница:

Последние рефераты