Формулы (62) и (63) называются интегральными формулами Вилля-Пуассона. Подставляя (62) и (63) в исходную интегральную (59) мы получим интегральную формулу Дирихле через интеграл Чизотти. Формулы (62) и (63) можно назвать интегральными формулами Дирихле-Чизотти для конечных двусвязных областей.

в) Интегральная формула Чизотти для заданных областей – решение

задачи Дирихле для соответствующих областей.

Если известны интегральные формулы Шварца для круговых областей , дающие аналитической в функции через нормальной производной ее действительной части на границе области и интегральные представления Чизотти для круговых областей, дающие выражение функции , реализующей конформное отображение области на ограниченную гладкой кривой (51), (52), то поэтому интегральную формулу, дающую конформное отображение на через нормальную (касательную) производную ее действительной (мнимой) части на границе , естественно назвать интегральной формулой Дини-Шварца-Чизотти для заданных областей.

Можно рассмотреть интегральные формулы Дини-Шварца для многосвязных областей и их применение к решению краевых задач типа Дирихле.

Решение задачи Неймана сводится к решению задачи Дирихле сопряженной гармонической функции.

Учитывая, что задача конформного отображения многосвязной области на каноническую область и задача Дирихле для той же области эквивалентны (49), используем интегральный метод Чизотти для соответствующих областей (50), (51).

Применяя ИПАФ типа Шварца регулярной и однозначной в , найдем решение задачи Дирихле, как представляющее однозначную и аналитическую (гармоническую) в произвольной многосвязной области функцию

(64)

удовлетворяющую в уравнению

(65)

и граничному условию

, , (66)

где .

Решение задачи (65) и (66) в заданных произвольных областей имеет следующий вид:

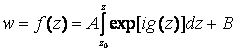(67)

или после соответствующих преобразований получим (§4 п."б"):

;

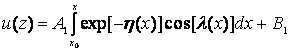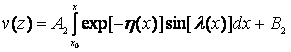, (68)

где и постоянные, определяемые нормировкой функции , - угол наклона касательной в точке , соответствующей при отображении .

Пусть теперь - каноническая область (круг, концентрическое круговое кольцо, внешность двух кругов, …), а - соответствующая область, ограниченная контуром .

Построим функцию , дающую конформное отображение на . Причем будем для простоты считать, что , .

В силу конформности отображения всюду в функция равна

; на (69)

,

Следовательно, функцию можно представить следующими интегральными формулами типа Шварца:

, , ();

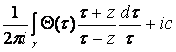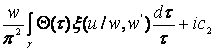, , (; (70)

, ,

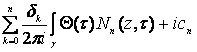где - ядро Шварца для круга;

- функция Вейерштрасса;

- ядро Александра-Сорокина для неконцентрического кругового кольца;

- ядро для внешности двух окружностей;

- ядро для симметричных и равных (неравных) окружностей.

Интегральное представление (68) назовем интегральной формулой для решения задачи типа Дирихле для рассмотренных областей .