Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам Дирихле

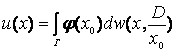, (9)

являющейся обобщением формулы (8). Здесь - гармоническая мера множества в точке . Отсюда возникает возможность рассмотрения обобщенной задачи Дирихле для произвольных граничных функций , при этом можно требовать удовлетворения граничного условия лишь в некоторой ослабленной форме.

Например, если - область с достаточно гладкой границей Г, а граничащая функция имеет только точки разрыва 1-го рода, то можно требовать удовлетворения граничного условия лишь в точках непрерывности , для обеспечения единственности решения в точках разрыва требуется ограниченность решения.

е) Задача Неймана.

Наряду с задачей Дирихле для некоторых приложений важно рассмотреть так называемую вторую краевую задачу, или задачу Неймана:

Найти гармоническую в области функцию , зная значения ее нормальной производной на границе С:

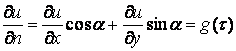(10)

и значение в какой-либо точке в области .

Для определенности мы будем предполагать, что в (10) рассматривается внешняя нормаль, что означает угол, образованный этой нормалью с осью х. Функция может иметь на конечное число точек разрыва 1-го рода, функция и ее частные производные первого порядка предполагаются ограниченными.

Следующая теорема выражает от нормальной производной гармонической функции:

Если функция гармонична в односвязной области и непрерывна вместе со своими частными производными в , то

, (11)

где - граница области обозначает производную в направлении нормали к , а - дифференциал дуги.

Из этой теоремы следует, что для разрешимости задачи Неймана необходимо выполнения соотношения

. (12)

Доказывается единственность решения задачи Неймана и при доказательстве единственности решения задачи Неймана можно ограничиться случаем, когда область представляет собой полуплоскость (z, > 0).

В дополнительном предположении непрерывности частных производных в решение задачи Неймана сводится к решению задачи Дирихле для сопряженной гармонической функции.

Две гармонические в области функции и , связанные условиями Даламбера-Эйлера называются сопряженными.

Как мы знаем, для всякой функции гармонической в односвязной области , можно найти сопряженную с ней гармоническую функцию . Так как функция определяется своими частными производными с точностью до постоянного слагаемого, то совокупность всех гармонических функций сопряженных с дает формула:

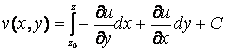, (13)

где С – произвольная действительная постоянная.

Заметим, что в многосвязной области интеграл (13) по контуру , определяет, вообще говоря, многозначную функцию:

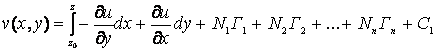, (14)

где - произвольные целые числа, а - интегралы вдоль замкнутых контуров , каждый из которых содержит внутри себя одну связную часть границы :

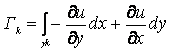. (15)

Постоянные называются периодами интеграла (13) или циклическими постоянными.

Можно доказать, что решение задачи Неймана сводится к решению задачи Дирихле для сопряженной гармонической функции , где , носят название соответственно силовой функции и потенциала поля.

Функции и , представляющие собой регулярные решения системы Коши-Римана [6]:

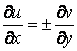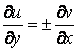
, (16)

имеют частные производные всех порядков, т.е. аналитические функции являются решением уравнения . (17)

Условие (17) – условие комплексной дифференцируемости функции .

Страница:

Последние рефераты