Функция регулярна и действительные части на граничных компонентах принимают непрерывные значения , определяемые равенством (65), а - ядро определяется следующими формулами [5]:

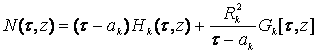, (76)

, (77)

-1, при , с – вещественное число.

Если мы в (67) отделим вещественную и мнимую части, то мы получим две интегральные формулы Пуассона для - связных круговых областей ; что мы и делаем, следуя вычислениям Александрова-Сорокина [5], т.е. решаем задачу Дирихле-Пуассона: об определении значений гармонической функции внутри канонической области , если известны ее значения на границах , - функция полярного аргумента, дающая граничные значения .

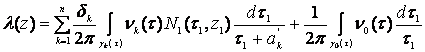, (78)

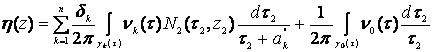, (79)

где , , .

Рассмотрим некоторые частные задачи Дирихле-Пуассона для .

Следствие 1. Если в формулах (72) и (73) положить , то мы получим формулу Пуассона – интеграл Пуассона для круга [ ]:

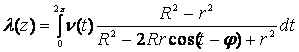, () (80)

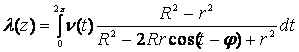, () (81)

Следствие 2. Если в формулах (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца:

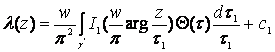, (82)

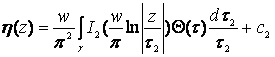, (83)

где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, ().

Так как функция ) представляется быстро сходящимися рядами, то формулы (74) и (75) можно с успехом использовать для приближенного решения соответствующих граничных задач.

Следствие 3. Если в формулах (70) и (71) - задана нормальная (касательная) производная, то мы получим две интегральные формулы Дини-Шварца для соответствующих областей, т.е. получим непосредственное обобщение интеграла Дини, дающее решение граничной задачи Неймана для заданных рассмотренных областей.

В случае единичного круга эта формула имеет вид[1, 9]:

, (84)

где действительная функция при , под понимается дифференцирование по направлению внутренней нормали, а с – произвольная постоянная. Формула (76) имеет место при условии, что

. (85)

Условие (77) – необходимое и достаточное условие дл разрешимости рассматриваемой граничной задачи и при его выполнении искомая однозначная аналитическая функция определяется с точностью до произвольного комплексного постоянного слагаемого.

А из (76) следуют формулы Дини:

.

В случае кругового кольца , имеем

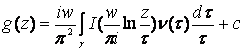, (87)

, .