Определители и системы линейных уравненийРефераты >> Математика >> Определители и системы линейных уравнений
и соответствующие равенства, относящиеся не к столбцам, а к строкам:
+
+
= 0, 
+
+
= 0,
+
+
= 0, 
+
+
= 0,
+
+
= 0, ++= 0.
2. Системы линейных уравнений с тремя неизвестными
2.1. Системы трех линейных уравнений с тремя неизвестными с определителем, отличным от нуля.
В качестве приложения изложенной выше теории рассмотрим систему трех линейных уравнений с тремя неизвестными:
|
+
+
= 
, 
+ +
= 
,
+ +
= 
,
(коэффициенты , , , , , , , , , и свободные члены , , считаются заданными). Тройка чисел 
, 
, 
называется решением системы (3.19), если подстановка этих чисел на место , 
, 
в систему (3.19) обращает все три уравнения (3.19) в тождества.
Фундаментальную роль в дальнейшем будут играть следующие четыре определителя:
= 
= 
= 
= 
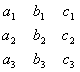
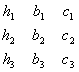
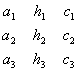
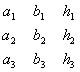
Определитель принято называть определителем системы (3.19) (он составлен из коэффициентов при неизвестных). Определители , и получаются из определителя системы посредством замены свободными членами элементов соответственно первого, второго и третьего столбцов.
