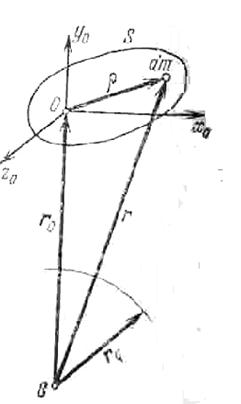
Рис. 3.5.

Найдем выражения, позволяющие вычислять составляющие вектора гравитационного момента Мгр, действующего на некоторое тело S [1, 3]. Введем связанную с телом правую систему координат ОXоYоZo с ортами i, j, k и началом в центре масс тела О, которая совпадает с орбитальной. Соответственно ось OYo натравим по продолжению радиуса-вектора, соединяющего центр притяжения С с началом О, а ось ОXo расположим в мгновенной орбитальной плоскости. Гравитационный момент, действующий на тело S, будет равен:

;

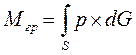где p - радиус-вектор некоторой элементарной массы материального тела,

dG-вектор силы тяжести, действующей на эту элементарную массу. Очевидно, что

.

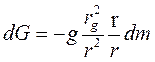Здесь g - ускорение силы тяжести на поверхности планеты, r – радиус-вектор элементарной массы dm относительно центра тяготения С, гg -удаление поверхности планеты от центра C. Введя еще r0 - радиус-вектор центра масс тела S относительно С, следовательно [3]:

;

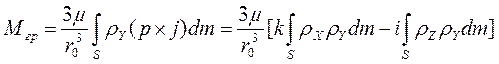где - гравитационная постоянная для рассматриваемой планеты, равная .

Проекции гравитационного момента на оси триэдра ОXoYoZo, будут равны:

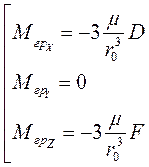; (3.18)

где D и F-центробежные моменты инерции тела S, определяемые для системы

осей ОXоYоZo.

Полученные для гравитационного момента выражения говорят о том, что вектор этого момента всегда лежит в плоскости местного горизонта (перпендикулярен к местной вертикали СО) [1, 4, 10]. Кроме того, очевидно, что гравитационный момент для тела, главные центральные оси инерции которого в данное мгновение совпадают с орбитальными, равен нулю (так как в этом случае D=F=0), в частности он всегда равен нулю для тела, эллипсоид инерции которого является сферой.

В общем случае главные центральные оси инерции тела могут быть повернуты произвольным образом относительно орбитальных осей ориентации. Обозначим жестко связанный с телом S триэдр, совпадающий с главными центральными осями инерции, через Охуz, а для орбитальных осей сохраним обозначение OXoYoZo. Взаимное положение этих систем координат определим следующей таблицей направляющих косинусов:

.

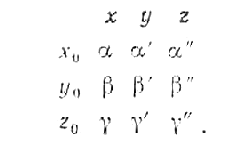Найдем проекцию гравитационного момента на ось Ох. Очевидно, что

. (3.19)

Воспользовавшись свойством направляющих косинусов, преобразуем равенство (3.19) с учетом формул (3.18):

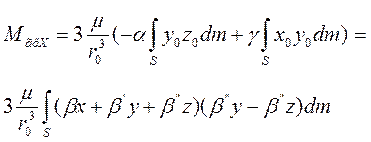; (3.20)

поскольку триэдр Oxyz совпадает с главными центральными осями инерции, постольку все центробежные моменты инерции в этих осях будут равны нулю, и выражение (3.20) может быть упрощено [1, 3]. Проделав аналогичные выкладки для нахождения проекций гравитационного момента можно, написать:

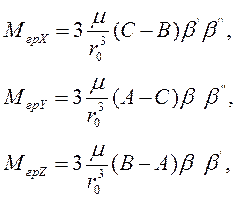(3.21)

Таким образом, гравитационный момент, действующий вокруг одной из осей триэдра Oxyz, зависит от разности моментов инерции относительно двух других осей. Чтобы сделать анализ полученных выражений более наглядным, рассмотрим гравитационный момент, действующий на тело S, при условии, что оси 0Z и 0Zo совпадают. Это соответствует повороту тела S, который можно назвать поворотом по тангажу, на угол (рис. 3.6).

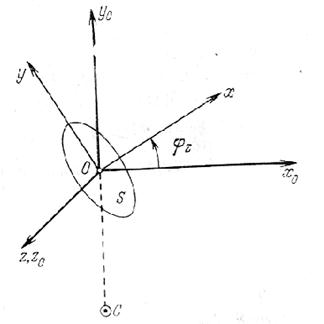
Рис. 3.6 - Поворот тела вокруг оси Z

При сделанных предположениях

, ;

н, следовательно,

;

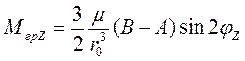Как и надо было ожидать, при гравитационный момент обращается в нуль, поскольку триэдры Охуz и 0XoYoZo в этом случае совпадают [1, 3]. При монотонном увеличении от гравитационный момент возрастает, достигает максимума при , затем убывает и вновь становится равным нулю при . Таким образом, существует два положения равновесия: при и при . Однако, из этих положений одно соответствует статической устойчивости (при малом изменении , возникает момент противоположного знака), другое – статистической неустойчивости. Действительно, производная

;

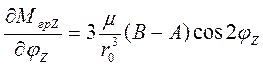при и при имеет разные знаки. Какое из этих двух положений соответствует статистической устойчивости, зависит от знака (B-A) [1, 3, 8]. Условие устойчивости (возникновение восстанавливающего момента при малом отклонении) 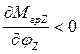реализуется при для A>B или при для B>A, т.е. в обоих случаях вытянутая ось тела должна занимать вертикальное положение.

Таким образом, вытянутое в вертикальном положении тело, обладая статистической устойчивостью по тангажу и крену, является нейтральным по отношению к углу рыскания [1, 3, 4].

3.3 Гироскопический измеритель угловой скорости

Для пересчета векторов сил, моментов и т.д. из одной системы координат в другую необходимо вычислить матрицу перехода, элементами которой являются косинусы углов между осями исходной и повернутой систем координат [1, 3, 21]. Эта матрица определяется последовательностью углов поворота, которые позволяют перейти от одной системы координат к другой. Осуществление такого рода перехода требует не более трех поворотов исходной системы координат. Выбор последовательности углов поворота обычно определяется физическим содержанием задачи [1, 3, 5]. Это могут быть углы, измеренные с помощью приборов системы управления, от которых зависят аэродинамические и другие нагрузки на ЛА и т.д. [1]