Разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппарата

Вероятность совершить ошибку l рода [8] называется уровнем значимости критерия и обозначается q. Обычно уровень значимости выбирают, равным 0.01; 0.1; 0.05 (последнее значение - наиболее часто) [28].

Критерии значимости – это критерии, с помощью которых проверяют гипотезы об абсолютных значениях параметров или о соотношениях между ними для генеральных совокупностей (с точностью до параметров) функцией распределения вероятностей [29].

Построение гистограммы выборки. Гистограмма является эмпирическим аналогом функции плотности распределения f(x). Обычно ее строят следующим образом:

1. Находят предварительное количество квантов (интервалов), на которое должна быть разбита ось Ox. Это количество K определяют с помощью оценочной формулы:

K=1+3.2lgN ; (4.34)

Где найденное значение округляют до ближайшего целого числа.

2. Определяют длину интервала [29]:

; (4.35)

Величину можно округлить для удобства вычислений.

3. Середину области изменения выборки (центр распределения) принимают за центр некоторого интервала, после чего легко находят границы и окончательное количество указанных интервалов так, чтобы в совокупности они перекрывали всю область от до .

4. Подсчитывают количество наблюдений попавшее в каждый квант; равно числу членов вариационного ряда, для которого справедливо неравенство [27-29]:

; (4.36)

здесь и - границы m-ого интервала. Отметим, что при использовании формулы (4.36) значения попавшее на границу между (m-1)-м и m-ом интервалами, относят к m-ому интервалу.

5. Подсчитывают относительное количество (относительную частоту) наблюдений /N , попавших в данный квант.

Строят гистограмму [7, 8, 9], представляющую собой ступенчатую кривую, значения которой на m-ом интервале , (m=1,2,…,K)

6. постоянно и равно /N, или с учетом условия 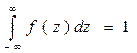равно (/N).

Критерии согласия. Критерием согласия [8] называется критерий гипотезы о том, что генеральная совокупность имеет распределение предполагаемого типа (например, нормально распределение). Среди различных критериев согласия наиболее употребителен универсальный критерий согласия (Пирсона).

Проверку гипотезы о виде функции распределения с помощью этого критерия производят следующим образом [27-29]:

1. a) По выборке строят гистограмму. Если в каком-либо f-ом интервале число наблюдений окажется меньше пяти, то его объединяют с соседним интервалом (или интервалами) так, чтобы число наблюдений в таком объединенном интервале оказалось большим или равным пяти. Пусть – окончательное число интервала группирования, тогда очевидно, что

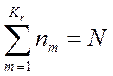; (4.37)

б) Задаются видом гипотетической функции распределения и для каждого из r (r=1,2,…) параметров этого распределения находят оценки, причем эти оценки можно определять как по исходным, так и по сгруппированным данным [27].

в) Определяют теоретическую вероятность попадания в каждый из интервалов случайной величины с заданным распределением, параметры которого или известны или оценены в параграфе б) [28].

г) вычисляют число g:

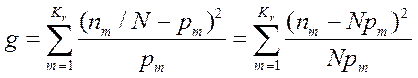; (4.38)

2. Известно, что для данного критерия согласия случайная величина g при Больших N имеет распределение с - r - 1 степенями свободы, где r - число определенных неизвестных заранее параметров гипотетического распределения, а уменьшения числа степеней свободы еще на единицу объясняется наличием линейного соотношения (4.35) между эмпирическими величинами и N , входящими в расчетную формулу (4.36). Задавшись уравнением значимости q, по таблице -распределений находят критическое значение , причем критическая область определяется неравенством g>==- r – 1;.

3.Сравнивая значения g и и выносят решение о принятии (g <=) или отклонение (g >) рассматриваемой гипотезы о виде функции распределения [27-29].

4.7 Алгоритм контроля отказов ДС при неполной тяге

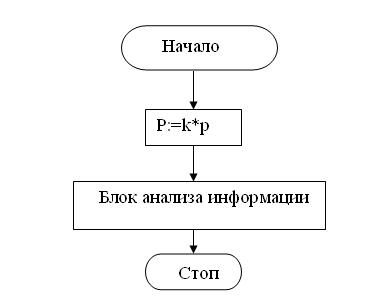
Алгоритм неполной тяги - представляет собой алгоритм позволяющий моделировать остаточную тягу при отказе одного из реактивных двигателей стабилизации, для отказа типа «не отключение». Остаточная тяга может меняться в пределах: 0%-100%. При 0% тяги, отказ типа «не отключение» переходит в отказ типа «не включение». Пусть P – тяга, а k – коэффициент остаточной тяги, задаваемый в процентах. Тогда в общем случае, при отказе одного из двигателей, тяга имеет вид (4.39) [25, 26]:

(4.39)

Блок-схема алгоритма имеет вид (Рис. 4.8):

Страница:

Последние рефераты