Доказательство. Для величин с дискретным распределением: пусть xk и yn — значения ξ и η, соответственно.

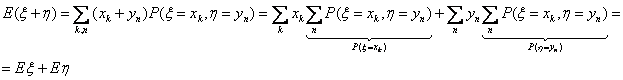
E5.Если ξ ³ 0 п.н. (« почти наверное», т.е. с вероятностью 1: P(ξ ³ 0 ) = 1), то E ξ ³ 0;

Если ξ ³ 0 п.н., и при этом Eξ = 0, то ξ = 0 п.н., то есть P(ξ = 0) = 1.

Следствие 11.

Если ξ £ η п.н., то E ξ £ Eη .

Если ξ £ η п.н., и при этом Eξ = Eη, то ξ = η п.н.

E6. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.: если ξ и η независимы, то

E(ξη) = Eξ Eη.

Доказательство.

Замечание 16. Обратное утверждение к свойству E6 неверно: из равенства E(ξη) = Eξ Eη. Не следует независимость величин ξ и η.

Пример 28. Пусть φ Î U0,2π, ξ = cos φ, η = sin φ— заведомо зависимые случайные величины. Но математическое ожидание их произведения равно произведению их математических ожиданий: по свойству E1

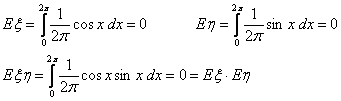
11.3 Моменты старших порядков. Дисперсия

Определение 40. Если , то число

называется моментом порядка k (k -м моментом) случайной величины ξ;

называется абсолютным моментом порядка k (абсолютным k -м моментом) случайной величины ξ;

называется центральным моментом порядка k (центральным k -м моментом) случайной величины ξ;

называется абсолютным центральным моментом порядка k (абсолютным центральным k -м моментом) случайной величины ξ.

Число Dξ = E(ξ – Eξ)2 (центральный момент порядка 2) называется дисперсией случайной величины ξ

Пример 29. Пусть, скажем, случайная величина ξ принимает значение 0 с вероятностью 1-10-5 , и значение 100 с вероятностью 10-5. Посмотрим, как моменты разных порядков реагируют на большие, но маловероятные значения случайной величины.

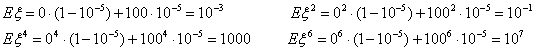
Пример 30. Дисперсия Dξ = E(ξ – Eξ)2 есть «среднее значение квадрата отклонения случайной величины ξ от своего среднего». Посмотрим, за что эта величина отвечает.

Пусть случайная величина ξ принимает значения +-1 с вероятностью 1/2, а случайная величина η — значения ю +-10 с вероятностью 1/2. Тогда Eξ = Eη = 0 поэтому D ξ = E ξ2 = 1, Dη = Eη2 = 100. Говорят, что дисперсия характеризует степень разброса значений случайной величины вокруг ее математического ожидания.

Если говорить о распределении случайной величины, как о распределении единичной массы по невесомому стержню, то дисперсия есть в точности момент инерции этого стержня, закрепленного в центре тяжести.

Определение 40. Если дисперсия величины ξ конечна, то число называют среднеквадратичным отклонением случайной величины ξ.

Следует хорошо понимать, что из существования моментов больших порядков следует существование моментов меньших порядков. В частности, конечность второго момента (или дисперсии) влечет существование математического ожидания.

11.4 Свойства дисперсии

Все свойства дисперсии следуют из соответствующих свойств математического ожидания.

D1.

Действительно,

D2.

D3.

если и только если ξ= const.п.н.

Доказательство. Дисперсия есть всего-навсего математическое ожидание п.н. неотрицательной с.в.:

Dξ = E(ξ – Eξ)2, и неотрицательность дисперсии следует из свойства E5. По тому же свойству, Dξ = 0 если и только если E(ξ – Eξ)2 = 0 п.н., то есть ξ = ξ п.н.

D4. Дисперсия не меняется от сдвига с.в. на постоянную:

D5. Если ξ и η независимы, то

Действительно,

так как математическое ожидание произведения независимых с.в. равно произведению их математических ожиданий.

D6. Минимум среднеквадратического отклонения случайной величины ξ от точек вещественной прямой есть среднеквадратическое отклонение ξ от своего математического ожидания:

Наименьший момент инерции стержня с распределенной на нем единичной массой получится, если точка вращения – центр тяжести стержня, а не любая другая точка.

Доказательство.

причем равенство достигается только для а = Eξ.

11.5 Математические ожидания и дисперсии стандартных распределений

Пример 31. Распределение Бернулли Вр,

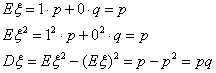
Пример 32. Биномиальное распределение Вn,p

Воспользуемся свойством устойчивости биномиального распределения относительно суммирования — леммой 5. Возьмем n независимых случайных величин ξ1 ξ2 … ξn, имеющих распределение Бернулли В,p = В1,p.

Тогда их сумма Sn = ξ1 + ξ2 +… + ξn имеет распределение Вn,p

так как все ξi одинаково распределены и их математическое ожидание равно pi;

поскольку ξi независимы и дисперсия каждой равна pq.

Пример 33. Геометрическое распределение Gp

При p Î (0,1)

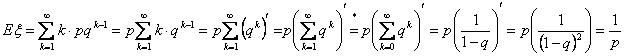
Равенство (*) появилось из-за нежелания дифференцировать сумму геометрической прогрессии, которая начинается не с 0 а с q. Заметьте, что производная у добавленных слагаемых равна 0, так что производные от этих двух сумм равны