Теорема 12. В n испытаниях схемы Бернулли с вероятностью успеха p наиболее вероятным числом успехов является

a) единственное число k0 = [np + p], если число np + p не целое;

б) два числа k0 = np + p и k0 -1= np + p -1, если число np + p целое.

Пример 19. Если p = q = 1/2, то при четном числе испытаний n число np + p = n/2 + 1 /2— не целое, так что наиболее вероятным является единственное число успехов [n/2 + 1 /2] = n/2. Что совершенно понятно, так как есть нечетное число возможностей — получить 0, 1, …n успехов, причем вероятности получить k и n-k успехов одинаковы.

При нечетном же числе испытаний n число np + p = n/2 + 1 /2 — целое, так что наиболее вероятными (и одинаково вероятными) являются два числа успехов n/2 + 1 /2 и n/2 - 1 /2.

5.3 Номер первого успешного испытания

Рассмотрим схему Бернулли с вероятностью успеха p в одном испытании. Испытания проводятся до появления первого успеха. Введем величину τ , равную номеру первого успешного испытания.

Теорема 13. Вероятность того, что первый успех произойдет в испытании с номером k, равна

P(τ = k) = p qk-1.

Доказательство. Действительно,

Определение 21. Набор чисел {p qk-1 } называется геометрическим распределением вероятностей и обозначается Gp или G(p).

Геометрическое распределение вероятностей обладает интересным свойством, которое можно назвать свойством «нестарения». Пусть величина τ обозначает, скажем, время безотказной работы (измеряемое целым числом часов) некоторого устройства. Предположим, что для величины τ вероятность принять любое свое значение k в точности равна pqk-1. Справедливо следующее утверждение.

Теорема 14. Пусть P(τ = k) = p qk-1. Тогда для произвольных n, k ³ 0

P(τ > n+k\ τ > n) = P(τ > k)

Данному равенству можно придать следующее звучание: если известно, что устройство проработало без отказов n часов, то вероятность ему работать еще не менее k часов точно такая же, как вероятность проработать не менее k часов для нового устройства.

Можно прочесть эту формулу и так: вероятность работающему устройству проработать еще сколько-то часов не зависит от того момента, когда мы начали отсчет времени, или от того, сколько уже работает устройство.

Доказательство. По определению условной вероятности,

(4)

Последнее равенство следует из того, что событие {τ > n+k} влечет событие {τ > n}, так что пересечение этих событий есть {τ > n+k}. Найдем для произвольного m ³ 0 вероятность P(τ > m).

Можно также заметить, что событие {τ > m} означает, что в схеме Бернулли первые m испытаний завершились «неудачами», а это событие имеет вероятность как раз qm.

Возвращаясь к (4), получим

5.4 Приближение гипергеометрического распределения биномиальным

Рассмотрим урну, содержащую N шаров, из которых K шаров — белые, а оставшиеся N-K шаров — черные. Из урны наудачу (без возвращения) выбираются n шаров. Вероятность PN,K(n, k) того, что будет выбрано ровно k белых и n-k черных шаров, находится по формуле (см. определение 8 гипергеометрического распределения вероятностей):

Если число шаров в урне очень велико, то извлечение одного, двух, трех шаров почти не меняет пропорцию белых и черных шаров в урне, так что вероятности PN,K(n, k) не очень отличаются от вероятностей в процедуре выбора с возвращением

P(получить ровно k белых шаров при выборе n шаров с возвращением) =

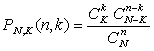Сформулируем нашу первую предельную теорему.

Теорема 15. Если N → ∞ и K → ∞ так, что K/N → p Î (0, 1) то для любых фиксированных n, 0<=k<=n

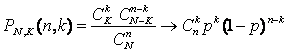5.5 Независимые испытания с несколькими исходами

Рассмотрим следующий пример, когда из двух очень похожих вопросов на один можно ответить, пользуясь формулой Бернулли, а для другого этой формулы оказывается недостаточно:

Пример 20. Игральная кость подбрасывается 15 раз. Найти вероятности следующих событий:

а) выпадет ровно 10 шестерок; б) выпадет ровно 10 шестерок и три единицы.

а) есть 15 испытаний схемы Бернулли с вероятностью успеха 1/6 (выпадение шестерки). Вероятность десяти успехов в 15 испытаниях равна

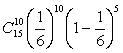
б) здесь каждое испытание имеет три, а не два исхода: выпадение шестерки, выпадение единицы, выпадение остальных граней. Воспользоваться формулой для числа успехов в схеме Бернулли не удается — перед нами уже не схема Бернулли.

Осталось изобрести формулу для подсчета вероятности каждому исходу в нескольких независимых испытаниях выпасть нужное число раз, если в одном испытании возможно не два, а более исходов.

Пусть в одном испытании возможны m исходов. Обозначим их цифрами 1, 2, …m. Пусть исход i в одном испытании случается с вероятностью рi, 1 ≤ i ≤ m и

Обозначим через Р(n1,n2,…,nm) вероятность того, что в n = n1+ n2+ …+nm независимых испытаний исход 1 появился n1, раз, исход 2 – n2 раз,…

Теорема 16. Для любого n и любых целых n1 ≥ 0… nm ≥ 0 таких, что n1+ n2+ …+nm = n, верна формула:

Доказательство. Рассмотрим один элементарный исход, благоприятствующий выпадению n1 единиц, n2 двоек, … , nm раз m-ок:

Это результат n экспериментов, когда все нужные исходы появились в некотором заранее заданном порядке. Вероятность такого результата n независимых испытаний равна