Говря о «силе» зависимости между с.в., мы имеем в виду следующее. Самая сильная зависимость – функциональная, а из функциональных – линейная зависимость, когда ξ= аη + b п.н. Бывают гораздо более слабые зависимости. Так, если по последовательности независимых случайных величин ξ1 ξ2 … построить ξ = ξ1 +…ξ24 + ξ25 η = ξ25 +ξ26 + …+ξ90 , то эти величины зависимы, но очень “слабо зависимы”: через одно-единственное общее слагаемое ξ25 .

Итак, следующая величина есть всего лишь ковариация, нормированная нужным образом.

12.2 Коэффициент корреляции

Определение 43. Коэффициентом корреляции ρ(ξ, η) случайных величин ξ, η, дисперсии которых существуют и отличны от нуля, называется число

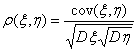
Пример 42. Рассмотрим продолжение примера 41, но пусть ξ и η будут не только независимыми, но и одинаково распределенными случайными величинами, и их дисперсия отлична от нуля. Найдем коэффициент корреляции величин ξ и ξ + η. Согласно формуле (10),

Поэтому

Определение 44. Случайные величины ξ и η называют некоррелированными, если cov(ξ, η) = 0 (или если ρ(ξ, η) = 0, — в том случае, когда коэффициент корреляции существует).

Замечание 17. Если одна из величин ξ и η — постоянная, то эти величины независимы, и cov (ξ, η) = 0. Естественно в этом случае тоже полагать, что ξ и η «некоррелированы», хотя коэффициент корреляции не определен (дисперсия постоянной равна 0).

12.3 Свойства коэффициента корреляции

Всюду далее специально не оговаривается, но предполагается, что коэффициент корреляции существует.

Теорема 26.

Коэффициент корреляции обладает следующими свойствами.

1. Если с. в. ξ и η независимы, то ρ(ξ, η) = cov(ξ, η) = 0.

2. ½ρ(ξ, η)½£. 1

3. ½ρ(ξ, η)½= 1, если и только если с. в. ξ и η с вероятностью 1 линейно связаны, т.е. существуют числа а ¹ 0 и b такие, что P(η = aξ+ b) = 1.

Определение 45. Пусть D конечна и отлична от нуля. Определим случайную величину

Преобразование называется стандартизацией случайной величины ξ, а сама с. в. называется стандартизованной , или (слэнг!) центрированной и нормированной версией с. в. ξ.

Свойство 13. Стандартизованная с. в. имеет нулевое математическое ожидание и единичную дисперсию.

Доказательство. Воспользуемся свойствами математического ожидания и дисперсии:

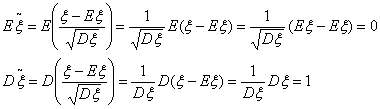
Полезно знать следующие часто употребляемые термины.

Определение 46. Говорят, что величины ξ и η отрицательно коррелированы, если ρ(ξ, η) < 0; говорят, что величины ξ и η положительно коррелированы, если ρ(ξ, η) > 0.

Смысл знака коэффициента корреляции особенно ясен в случае ½ρ(ξ, η) ½= 1. Тогда знак ρ равен знаку a в равенстве η = aξ+ b п.н. То есть ρ(ξ, η) = 1 означает, что чем больше ξ, тем больше и η. Напротив, ρ(ξ, η) = -1 означает, что чем больше ξ, тем меньше η. Похожим образом можно трактовать знак коэффициента корреляции и в случае, когда ½ρ(ξ, η) ½< 1, помня при этом, что зависимость величин ξ и η теперь уже не линейная и, возможно, даже не функциональная.

Так, величины ξ и ξ + η в примерах 41 и 42 положительно коррелированы, но их зависимость не функциональная.

Пример 43.

Если с. в. ξ и η есть координаты точки, брошенной наудачу в треугольник с вершинами (2,0), (0,0) и (0,1), то коэффициент корреляции ρ(ξ, η) отрицателен. Это можно объяснить «на пальцах» так: Чем больше ξ, тем меньше у η возможностей быть большой) Предлагаю убедиться в этом, проверив справедливость следующих высказываний.

Во-первых,

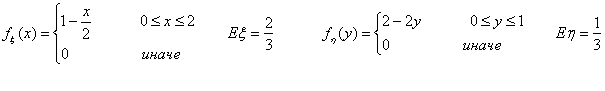
Во-вторых,

Совместное распределение координат точки, брошенной наудачу в произвольную (измеримую) область D на плоскости имеет постоянную плотность во всех точках области D. Это связано с понятием «наудачу»: вероятность попасть в любую область AÌ D, с одной стороны зависит только от площади А и не зависит от формы и положения А внутри D, равняясь с другой стороны, интегралу по области А от плотности совместного распределения координат точки. Эти два качества возможно совместить, только если плотность совместного распределения постоянна внутри D. Более того, эта постоянная, как легко видеть, есть просто (хотя бы потому, что интеграл от нее по всей области D должен ровняться вероятности попасть в D, или единице).

Распределение точки, брошенной наудачу в область (все равно где), называют равномерным распределением.

Итак, плотность равномерного распределения в произвольной области на плоскости — постоянная, равная (1/ площадь области) для точек внутри области и нулю — вне. Поэтому (а также потому, что площадь этого треугольника равна 1)

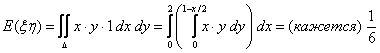
То есть ковариация (а с ней и коэффициент корреляции) отрицательна (посчитать cov(ξ, η)).

Пример 44.

Найти коэффициент корреляции между числом выпадений единицы и числом выпадений шестерки при n подбрасываниях симметричного кубика.

Решение. Обозначим для i = 1, 2, 3, 4, 5, 6 через ξi случайную величину, равную числу выпадений грани с i очками при n подбрасываниях кубика. Посчитаем cov(ξ1, ξ6).

Каждая из случайных величин ξi имеет биномиальное распределение с параметрами n и 1/6, поэтому

.

Заметим, что сумма ξ1 + … + ξn этих величин равна n. В силу симметрии кубика, все математические ожидания одинаковы, но, скорее всего, отличаются от

Посчитаем