Говорят, что эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если пространство элементарных исходов состоит из конечного числа │А│ = N равновозможных исходов.

В этом случае вероятность любого события А вычисляется по формуле

называемой классическим определением вероятности. Эта формула читается так: «вероятность события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов».

Замечание 5. Полезно помнить классическую формулировку Якоба Бернулли: «Вероятность есть степень достоверности и отличается от нее как часть от целого». (Ars Conjectandi, 1713 г.)

Замечание 6. Мы видим теперь, что подсчет вероятности в классической схеме сводится к подсчету числа «шансов» (элементарных исходов), благоприятствующих какому-либо событию, и общего числа шансов. Как правило, это делается с помощью формул комбинаторики.

Рассмотрим описанные в параграфе 1.1 урновые схемы. Напомним, что речь идет об извлечении k шариков из урны, содержащей n шариков. При этом три схемы: с возвращением и с учетом порядка, без возвращения и с учетом порядка, а также без возвращения и без учета порядка удовлетворяют классическому определению вероятности.

Общее число элементарных исходов в этих схемах подсчитано в теоремах 4, 2, 3 и равно, соответственно,

Четвертая же схема — схема выбора с возвращением и без учета порядка — имеет заведомо неравновозможные исходы.

Пример 6. Рассмотрим, скажем, выбор двух шариков из двух или, что то же самое, дважды подбросим монету. Если учитывать порядок, то исходов получится 4, и все они равновозможны, то есть имеют вероятность по 1/4:

(герб, герб), (решка, решка), (решка, герб), (герб, решка).

Если порядок не учитывать, то следует объявить два последних исхода одним и тем же результатом эксперимента, и получить три исхода вместо четырех: выпало два герба, либо две решки, либо один герб и одна решка.

При этом первые два исхода имеют вероятность 1/4, а последний — вероятность 1/4+1/4=1/2.

Гипергеометрическое распределение

Пример 7.

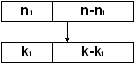Из урны, в которой n1 белых и n -n1 чёрных шаров, наудачу, без возвращения вынимают k шаров, k<n. Термин «наудачу» означает, что появление любого набора из k шаров равно возможно. Найти вероятность того, что будет выбрано ровно k1 белых и k - k1 чёрных шаров.

Заметим, что при k1 > n1 или k - k1 > n - n1 искомая вероятность равна 0, так как соответствующее событие невозможно. Пусть k1 < n1 и k - k1 < n - n1. Результатом эксперимента является набор из k шаров. При этом можно не учитывать или учитывать порядок следования шаров.

1. Выбор без учета порядка. Общее число элементарных исходов есть число k –элементных подмножеств множества, состоящего из n элементов, то есть (по теореме 3).

Обозначим через A событие, вероятность которого требуется найти. Событию A благоприятствует появление любого набора, содержащего k1 белых шаров и k - k1 черных.

Число благоприятных исходов равно произведению (по теореме 1) числа способов выбрать k1 белых шаров из n1 и числа способов выбрать k - k1 черных шаров из n - n1:

Вероятность события A равна:

2. Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместить n элементов на k местах (по теореме 2).

При подсчете числа благоприятных исходов нужно учесть, как число способов выбрать нужное число шаров, так и число способов расположить эти шары среди k. Можно, скажем, посчитать число способов выбрать k1 мест среди k (равное ), затем число способов разместить на этих k1 местах n1 белых шаров (равное — не забывайте про учет порядка!), и затем число способов разместить на оставшихся k - k1 местах n - n1 черных шаров (равное ). Перемножив эти числа, получим:

В рассмотренной задаче мы сопоставили каждому набору из k1 белых и k-k1черных шаров вероятность получить этот набор при выборе k шаров из урны, содержащей n1белых и n-n1черных шаров:

Определение 8. Соответствие или следующий набор вероятностей

Называется гипергеометрическим распределением.

Раздел 2. Геометрическая вероятность

2.1 Что это такое

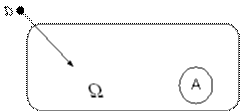Рассмотрим какую-нибудь область Ω в Rm ,(на прямой, на плоскости, в пространстве). Предположим, что «мера» Ω (длина, площадь, объем, соответственно) конечна. Пусть случайный эксперимент состоит в том, что мы наудачу бросаем в эту область точку а. Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от «меры» области.

Определение 9. Эксперимент удовлетворяет условиям «геометрического определения вероятности», если его исходы можно изобразить точками некоторой области Ω в Rm так, что вероятность попадания точки в любую А Í Ω не зависит от формы или расположения А внутри Ω, а зависит лишь от меры области А (и, следовательно, пропорциональна этой мере):

«Мерой» мы пока будем называть длину, площадь, объем и т.д.