Электродинамический принцип относительности
а следовательно,
F
где 
— некоторые постоянные, которые нам еще предстоит найти.
Итак, мы показали, что исходная функция 
имеет следующий вид:
где — некоторые пока не определенные постоянные.
Нахождение функции 
. Найдем теперь аналогичным образом функцию . Три основных соотношения для системы отсчета 
представим в виде:
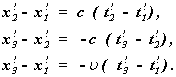
Вычитывая первое соотношение из третьего и сравнивая результат со вторым соотношением, получаем уравнение
т.е. уравнение
Видим, что функция удовлетворяет следующему функциональному уравнению:
в котором величины 
не независимые, а связаны нашими основными соотношениями для системы отсчета К. Используя эти соотношения, оставим независимыми только следующие три величины 
и
. Величины 
и 
выразим через указанные величины:
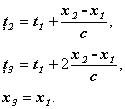
Таким образом, приходим к следующему основному функциональному уравнению для искомой функции:
которое выполняется при произвольных значениях и
.
Приступим к решению полученного функционального уравнения. Начнем с того, что продифференцируем его по 
:
производная последнего, третьего слагаемого в исходном функциональном уравнении равна нулю, так как оно не зависит от 
. Положим теперь в выведенном уравнении,
и тогда придем к дифференциальному уравнению
или уравнение
Легко найти общее решение последнего дифференциального уравнения. Для этого надо перейти только к новым независимым переменным
и показать, что в новых переменных уравнение имеет вид
Таким образом получаем общее решение нашего дифференциального уравнения:
в котором 
— пока произвольная функция.
Найдем вид этой функции. Подставим полученное выражение для функции в продифференцированное функциональное уравнение. Получим тогда соотношение
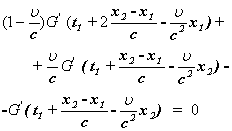
или соотношение
Так как аргументы у функций в правой и левой частях равенства при произвольных значениях
и
совершенно произвольны, то получаем, что
а следовательно,
где 
— пока неопределенные постоянные.
Определение констант 
. Мы получили, что формулы преобразований координат и времен произвольного мгновенного точечного события в инерциальных системах отсчета и имеют вид
Для нахождения констант привлечем дополнительное требование.
Требование 1. Предположим, что общие начала отсчета координат и времени в системах отсчета K и согласованы таким образом, что мгновенное точечное событие с координатами 0,0 в системе отсчета K имеет в системе отсчета координаты 0,0 ( тоже нулевые координаты),и наоборот.
Применяя вышеприведенные формулы преобразования к событию 0,0 получаем, что 
и поэтому формулы преобразования координат мгновенно точечного события приобретают следующий вид:
Теперь неопределенными остались только константы 
и 
.
Учтем теперь то обстоятельство, что формулы преобразования мы получили как следствия наших шести основных соотношений. Подставим поэтому полученные простые формулы обратно в эти исходные основные соотношения и установим ограничения на значения констант 
и . Имеем:
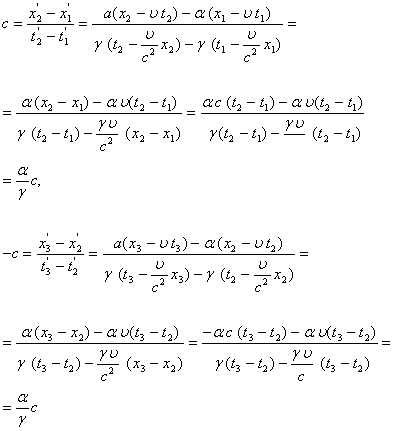
Таким образом, приходим к заключению, что константы и равны друг другу:
