Атомические разложения функций в пространстве Харди

Рефераты >> Математика >> Атомические разложения функций в пространстве Харди

В замечании 3 уже говорилось о том, что при пространство совпадает с пространством и из утверждения 2 следует, что

().

Последнее соотношение теряет силу при - нетрудно проверить, что при

,

где

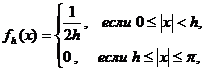
и, следовательно, существует функция , для которой . Таким образом, - собственное подпространство в . Ниже мы дадим критерий принадлежности функций к пространству .

ОпределениеII. 8.

Множество мы будем называть обобщенным интервалом, если - дуга на единичной окружности, т.е. - либо интервал из , либо множество вида

(). (69)

Точку назовем центром обобщенного интервала , если - центр дуги . Длиной обобщенного интервала естественно назвать величину

Определение II.9.

Действительную функцию назовем атомом, если существует обобщенный интервал такой, что

а) ;

б) ;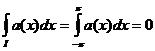

в) .

Атомом назовем также функцию , .

Теорема 8.

Для того, чтобы выполнялось включение: , необходимо и достаточно, чтобы функция допускала представление в виде*)

, , (70)

где , , - атомы. При этом

, (71)

где inf берется по всем разложениям вида (70) функции , а с и С - абсолютные константы.

Доказательство.

Достаточность.

Пусть для функции нашлось разложение вида (70). Покажем, что и . Для этого достаточно проверить, что для любого атома имеет место неравенство

. (72)

Пусть - такой обобщенный интервал, что

, , (73)

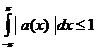(случай тривиален). Так как , то нам остается доказать, что

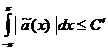. (74)

Для любого измеримого множества , применяя неравенство Коши и пользуясь утверждением 2 и соотношениями (73), мы находим

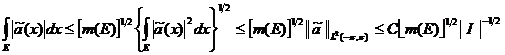, (75)

откуда сразу вытекает (74), в случае, когда .

Допустим теперь, что , и обозначим через обобщенный интервал длины с тем же центром, что и . Из (75) следует, что

.

Нам остается оценить интеграл . Мы воспользуемся очевидным неравенством

, ,

где - длина наименьшей из двух дуг единичной окружности, соединяющих точки и , а - абсолютная постоянная. В силу (73) при мы имеем

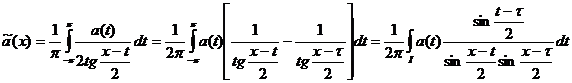где - центр обобщенного интервала . Из последнего соотношения, учитывая, что и , мы находим