.

Тогда для

.

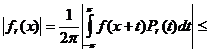
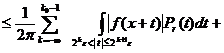
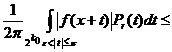
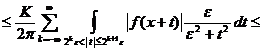
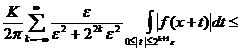
Неравенство (13) доказано. Возьмем слабый тип (1,1) оператора . Используя его, найдем такую последовательность функций ,что

,

( 14 )

для п.в. .

Согласно (13) при xÎ (-p,p)

Учитывая , что по теореме 1 для каждого xÎ [-p, p] и (14)

из последней оценки получим

при r®1.

Теорема 2 доказана.

Замечание1.

Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p, p] , когда точка reit стремится к eix по некасательному к окружности пути.

§I.2.Пространства Hp.

Определение I.3.

Пространство - совокупность аналитических в единичном круге функций F (z) , для которых конечна норма 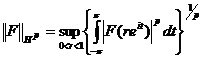. (15)

Пусть комплекснозначная функция удовлетворяет условиям (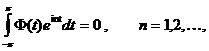16)

тогда функция F (z) , определенная равенством

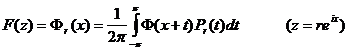(17)

принадлежит пространству , причем

. (18)

Действительно, аналитичность функции F (z) следует из (16) и равенства (2). Кроме того, в силу неравенства мы имеем

(*)

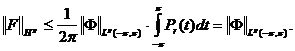С другой стороны , по теореме 1 ( а при р=¥ в силу теоремы 2)

. Отсюда (**)

Учитывая (*) и (**) , получим (18).

Ниже мы докажем, что любую функцию можно представить в виде (17). Для этого нам потребуется

Теорема 3.

Пусть комплекснозначная функция j (t) имеет ограниченную вариацию на [ -p,p] и

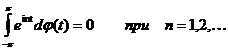(19)

Тогда j (t) абсолютно непрерывна на [-p,p].

Замечание2.

В (19) и ниже рассматривается интеграл Лебега-Стилтьеса, построенный по комплекснозначной функции ограниченной вариации j (t) . Мы говорим, что

j (t)= u (t)+ i v (t) имеет ограниченную вариацию (абсолютно непрерывна), если обе действительные функции u (t) и v (t) имеют ограниченную вариацию (соответственно абсолютно непрерывны). При этом интеграл

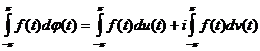
определен для каждой непрерывной на [-p,p] функции f (t) , а также если

- характеристическая функция замкнутого множества .

Доказательство теоремы 3.

Нам достаточно проверить, что для любого замкнутого множества ,

,

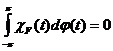(20)

Для этой цели убедимся, что справедлива

Лемма 1.

Пусть F - замкнутое, а V - открытое множества , причем и

. Тогда для всякого , существует функция вида

, (21)

обладающая свойствами:

а) ;

б) ; (22)

в) .

Выведем из леммы 1 оценку (20), а затем докажем саму лемму 1.

Пусть , где - конечная или бесконечная последовательность дополнительных интервалов множества F, и для

.

Очевидно, что - открытое множество и .

Рассмотрим для данных функцию , построенную в лемме 1 для числа e и множества . Тогда нетрудно проверить[3], что если , а , то разность

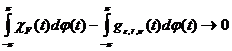. (23)