Определение3. Две гармонические функции и , связанные условиями Коши-Римана : , , называются гармонически сопряженными функциями.

Определение4. Под нормой пространства понимается

, .

Определение5. Под нормой пространства понимается

, .

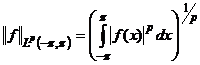Определение6. Пусть ( или ,). Модуль непрерывности ( соответственно интегральный модуль непрерывности) функции определяется равенством

, .

(, ).

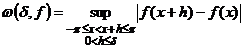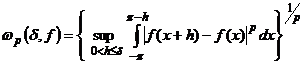Определение7. Последовательность функций, определенных на множестве Х с заданной на нем мерой, называется сходящейся почти всюду к функции , если для почти всех , т.е. множество тех точек , в которых данное соотношение не выполняется, имеет меру нуль.

В §I.2 мы рассматриваем пространства - это совокупность аналитических в единичном круге функций F (z) , для которых конечна норма

.

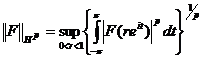Основным результатом этого параграфа является теорема о том, что любую функцию () можно предсавить в виде

, , ,

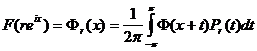где для п.в. , при этом

;

.

Использованные в данном параграфе понятия мы принимаем в следующих определениях:

Определение8. Говорят, что действительная функция , заданная на отрезке [a,b], имеет ограниченную вариацию, если существует такая постоянная , что каково бы ни было разбиение отрезка [a,b] точками выполнено неравенство .

Определение9. Действительная функция , заданная на отрезке [a,b], называется абсолютно непрерывной на [a,b], если для любого найдется число такое, что какова бы ни была система попарно непересекающихся интервалов , с суммой длин, меньшей : , выполняется неравенство .

В третьем параграфе первой главы мы переходим к рассмотрению пространств и . Пространство () представляет собой совокупность тех функций , , которые являются граничными значениями функций (действительных частей функций) из, т.е. представимы в виде (). Здесь мы получаем следующие результаты: при пространство совпадает с , а при р=1 уже, чем , и состоит из функций , для которых и .

В §I.4 мы вводим понятие произведения Бляшке функции , аналитической в круге с нулями , () с учетом их кратности:

,

где - кратность нуля функции при .

Здесь доказывается, что каждая функция представима в виде

, где не имеет нулей в круге и , ,а - произведение Бляшке функции .