Атомические разложения функций в пространстве Харди

Рефераты >> Математика >> Атомические разложения функций в пространстве Харди

, . (86)

Из неравенств (86) согласно (75') следует, что

при . (87)

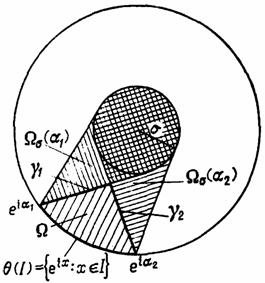
Легко видеть (учитывая, что и ) , что множества и пересекаются в одной точке:

с , . (88)

Пусть , , - отрезок, соединяющий точки и . Так как , , то из непрерывности функции при и неравенства (87) вытекает, что , если , , и . Поэтому , учитывая (88)

, ,, . (89)

По теореме Коши [5] .

Отсюда и из (89), учитывая, что для любой дуги справедливо равенство ,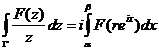

мы получим

.

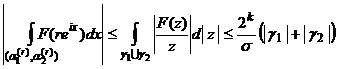Но в силу теорем 4 и 5

, ,

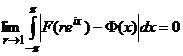и так как , , то мы находим, что

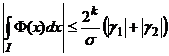. (89')

Легко видеть, что отношение ограничено сверху числом, зависящим только от s, поэтому

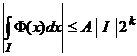, . (90)

Так как , то из соотношений (90) и (80) вытекает, что для , , справедливо неравенство (85). Для п.в. неравенство (85) сразу следует из определения функций и множеств .

Пользуясь оценкой (85) , из (83) мы получаем, что , а это значит, что функции

, , ,

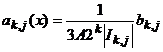являются атомами. Тогда, преобразуя неравенство (82), мы получаем разложение функции на атомы:

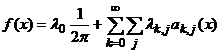для п.в. ,

где , .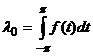

Оценим сумму модулей коэффициентов указанного разложения. Учитывая равенство (77), имеем

.

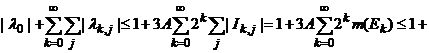
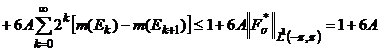Неравенство (76), а потому и теорема 8 доказаны.

§II.2. Линейные ограниченные функционалы на , двойственность и ВМО.

Дадим описание пространства , сопряженного к банахову пространству . Нам потребуется

Определение II.10.

Пространство ВМО есть совокупность всех функций , удовлетворяющих условию

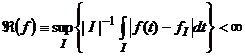, (91)

где , а sup берется по всем обобщенным интервалам .

Нетрудно убедится, что ВМО является банаховым пространством с нормой

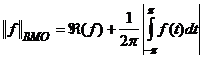. (92)

Ясно, что . В то же время ВМО содержит и неограниченные функции. Нетрудно проверить, например, что функция .