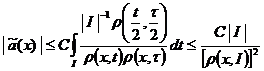, , где .

Следовательно,

.

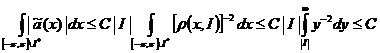Оценка (74), а потому и оценка (72) доказаны.

Необходимость.

Построим для данной функции разложение (70), для которого

.

Пусть функция с такова, что выполнено соотношение (65), и пусть () - нетангенциальная максимальная функция для , т.е.

, , (75')

где - область, ограниченная двумя касательными, проведенными из точки к окружности , и наибольшей дугой окружности , заключенной между точками касания.

Теорема 7 утверждает, что , поэтому нам достаточно найти такое разложение функции на атомы (70), что

, (76)

где постоянные С и () не зависят от . Для построения разложения (70) с условием (76) фиксируем число : пусть, например, . Не ограничивая общности, мы можем считать, что

. (77)

Рассмотрим на отрезке множества

, , (78)

Так как при любом множество точек единичной окружности открыто, то ясно, что при множество (если оно непустое) представимо (единственным образом) в виде суммы непересекающихся обобщенных интервалов:

, при , , . (79)

Положим 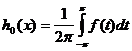и при

(80)

Так как конечна для п.в. , то из определения функций , , следует, что для п.в. при , а значит, для п.в.

.

Отсюда, учитывая, что , а следовательно из (80), при , мы находим, что

, (81)

где - характеристическая функция множества . Из (81), учитывая, что , мы для функции получаем следующее разложение:

для п.в. , (82)

где

, , (83)

С помощью функций мы и построим нужное нам разложение вида (70). Прежде всего отметим, что при ,

, . (84)

Докажем теперь, что для п.в.

, , (85)

где постоянная зависит только от числа , зафиксированного нами ранее.

Так как из (65) и (75') для п.в. , то из (77) следует, что

.

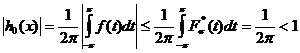Пусть теперь , - один из обобщенных интервалов в представлении (79), тогда из (77) и (78) , и если , - концевые точки дуги () , то , а значит,