НейрокомпьютерыРефераты >> Информатика >> Нейрокомпьютеры
Далее учтем и то, что единственным достоверно установленным на сегодняшний день информативным параметром выходных спайков является величина их межимпульсных интервалов, т. е. частота следования нервных импульсов в функции от величины возбуждения нервной клетки.
Таким образом, в качестве выходных величин нервных клеток следует рассматривать не сами спайки и, естественно, не аппроксимирующие их сигналы прямоугольной формы e(t), а частоты их следования, которые в свою очередь отражают степень возбуждения нейрона в каждый момент непрерывного времени t. Более того, выходная функция Z(t) нейрона может быть представлена при этом либо в виде частоты следования сигналов e(t), либо непосредственно в виде аналоговых величин или цифровых кодов, отражающих степень возбуждения нервной клетки. При таком подходе три последних уравнения математической модели (8) можно заменить одним уравнением следующего типа:
Z(t) = max{0, k[P(t) - Qп]}, (9)
где Z(t) – частота, пропорциональная возбуждению P(t) - Qп нейрона либо кодирующая ее аналоговая или цифровая величина; k – коэффициент пропорциональности; max{0, k[P(t) - Qп]} – функция, выделяющая те интервалы изменения P(t), на которых справедливо нестрогое равенство P(t)³ Qп.
Очевидно, что если функция (9) является выходной, то для взаимосвязанных и взаимодействующих нейронов значения Z(t) должны служить и в качестве входных. Обозначая входные величины как xj(t), представим алгоритм информационных процессов в нервной клетке в виде более простой, чем (8), но эквивалентной ей математической модели:
|
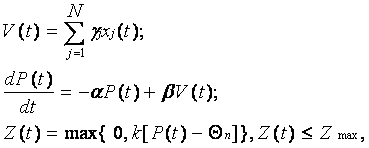 |
где xj(t) – аналог интенсивности входных воздействий, поступающих на j-й вход нейрона с синаптическим весом gj; V(t) – аналог потенциала, характеризующего суммарное входное воздействие, получаемое в результате пространственной суммации; P(t) – аналог мембранного потенциала нейрона; Qп – аналог постоянного порогового потенциала нервной клетки; a =1/t; b=aki ; ki – коэффициент пропорциональности при V(t); Zmax - максимально возможное значение Z(t), определяемое абсолютной рефрактерностью моделируемой клетки.
Вводя в систему (10) обозначение возбудимости нейрона в виде функции
y(t) = P(t) – Qп, (11)
получим идеализированную математическую модель информационных процессов в нервной клетке, которая имеет следующий вид:
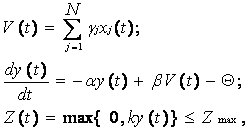 |
|
Как и в модели (8), первое уравнение системы (12) описывает процесс пространственной суммации входных воздействий, но не в форме единичных спайков, а в более общей форме величин, имеющих смысл мгновенных частот их следования. Второе уравнение описывает закон изменения возбудимости нейрона y(t), а третье – определяет процесс формирования выходных величин, характеризующих текущее возбуждение нервной клетки.
Математическую модель (12) можно использовать для построения нейроподобных элементов и цифровых нейропроцессоров.
3.Модели адаптивных процессов в нейроне
Адаптация, или приспособление к изменяющимся условиям внешней среды, является одним из наиболее важных свойств всего живого. Это свойство проявляется не только на уровне всего организма, но и на уровне отдельных его подсистем, отдельных клеток и внутриклеточных образований. На этом основании были разработаны модели нейронов, описывающие адаптивные реакции нейрона. Суть таких реакций заключается в плавном понижении частоты выходной импульсации в ответ на продолжительное стационарное внешнее воздействие, имеющее вид ступенчатой функции. Переходная характеристика адаптивной модели в этом случае соответствует кривой 1 на рисунке 1. Кривая 2 на том же рисунке обозначает реакцию на то же входное воздействие V(t) неадаптивного нейрона.
Другим типом адаптивных реакций являются так называемые “on”, “off” и “on–off” ответы нервных клеток. Они наиболее характерны для рецепторных нейронов зрительного анализатора и возникают при световом раздражении сетчатки глаза.
По виду переходные характеристики “on”, “off” ответов отличаются от кривой 1 на рисунке 1 тем, что при возрастании времени t они довольно быстро стремятся к нулю, а не к некоторой, отличной от нуля, постоянной величине. Последнее обстоятельство приводит к выводу о возможности воспроизведения адаптивных “on”, “off” ответов путем дифференцирования реакций неадаптивного нейрона, а именно кривых типа 2 на рисунке 1. Действительно, в этом случае выходные импульсные последовательности будут появляться в моменты начала и окончания ступенчатого входного воздействия, что и соответствует “on”, “off” ответам нейрона. Легко показать, что такой простейший механизм адаптивного поведения можно воспроизвести при помощи математической модели (12) практически без ее усложнения.
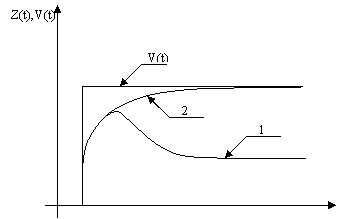 |
Рис. 1. Переходные характеристики.
Пусть суммарное входное воздействие V(t), поступающее на синаптические входы нейрона, представляет собой ступенчатый сигнал h, определяемый соотношением:
|
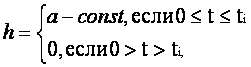 |
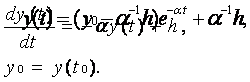 |
график которой совпадает с переходной характеристикой неадаптивной модели нейрона. Именно по этой причине устройство, реализующее алгоритм (12), может использоваться как искусственный неадаптивный нейрон.
