Аксиоматика векторного пространстваРефераты >> Математика >> Аксиоматика векторного пространства
По формуле треугольника ![]() и
и ![]() .
.
Так как X – середина ВС, М – середина CD, то ![]() и
и ![]() , и получаем систему:
, и получаем систему:
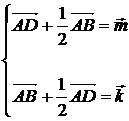
![]() , откуда
, откуда
![]()
Ответ: 4.
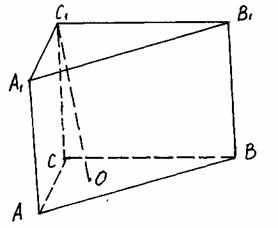
Задача. Ребра СА, СВ, СС, треугольной призмы ABCA1В1С1 равны, соответственно 2, 3 и 4 образуют между собой углы ![]() ACB = 90°,
ACB = 90°, ![]() ACС1 = 45° и
ACС1 = 45° и ![]() BCC1 = 60°. Найдите объём призмы.
BCC1 = 60°. Найдите объём призмы.
|
|
Решение.
Пусть отрезок С1О является высотой данной призмы. Тогда ![]()
Для того, чтобы найти высоту С1О, выберем в качестве базиса векторы
![]() и составим
и составим
таблицу умножения.
| * |
|
|
|
|
| 4 | 0 |
|
|
| 0 | 9 | 6 |
|
|
| 6 | 16 |
Разложим вектор C1O по векторам ![]() . Получим:
. Получим: ![]() , где
, где ![]() , а
, а ![]() .
.
Таким образом ![]() .
.
Коэффициенты х, у находим из условий перпендикулярности вектора C1O с векторами ![]() .
.
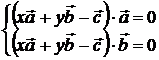
![]()
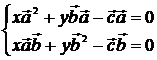
![]()
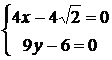
![]()
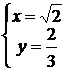 .
.
Следовательно, ![]()
Значит С1О = 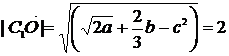
Тогда V = 3·C1O = 3·2 = 6
Ответ: 6.
С помощью векторов можно решать не только геометрические задачи, но и доказывать алгебраические неравенства.
I. Доказать неравенство ![]()
Доказательство:
Рассмотрим векторы ![]() и
и ![]() .
.
Их скалярное произведение ![]()
Так как ![]() ,
, ![]() , то, учитывая неравенство
, то, учитывая неравенство ![]() , получим
, получим ![]() .
.
II. Докажем, что для любых неотрицательных чисел a, b, c справедливо неравенство:
![]()
Доказательство:
Рассмотрим векторы ![]() и
и ![]() . Их скалярное произведение:
. Их скалярное произведение: ![]() , а длины
, а длины ![]() и
и ![]() . Отсюда, учитывая неравенство
. Отсюда, учитывая неравенство ![]() , получаем
, получаем
![]() .
.