Аксиоматика векторного пространства

Рефераты >> Математика >> Аксиоматика векторного пространства

Теорема 2.2. Для любого вектора существует единственный противоположный вектор .

Или:

и

Доказательство:

Допустим, что и и , т.е. существует , имеющий два различных противоположных вектора и .

и (1)

(2)

Тогда

и (3)

Левые части равенств (3) равны между собой. Действительно:

(4)

Из равенства (3) и (4) следует, что .

Теорема 2.3. Для любых векторов и существует единственный вектор , такой, что .

Доказательство:

I. Существование. Убедимся, что в качестве вектора можно будет выбрать вектор . В самом деле,

Таким образом, для векторов и существует вектор , удовлетворяющий равенству:

.

II. Единственность (от противного). Пусть

и (1)

Тогда:

Отсюда . Получим противоречие с допущением. Таким образом, единственность вектора доказана.

Определение 2.1. Вектор, удовлетворяющий равенству , называется разностью векторов и , и обозначается через - .

Таким образом

Теорема 2.3., как видно, вводит на множестве v новую операцию "–":

называемую вычитанием, которая является обратной по отношению к операции сложения.

Следствие 1.

Теорема 2.4.

Доказательство:

, т.к. - вектор, противоположный вектору . Тогда

Ч.т.д.

Теорема 2.5.

Доказательство:

Имеем:

;

Отсюда следует, что .

Ч.т.д.

Теорема 2.6. .

Доказательство:

Имеем:

Отсюда следует, что .

Теорема 2.7.

Доказательство:

Имеем:

(по Теореме 2.6.)

Отсюда следует, что .

Следствие 2. .

Теорема 2.8. или .

Доказательство:

Возможны два случая:

I. и

II. .

I. Если , то дизъюнкция или истинна и теорема доказана.

II. Пусть . Тогда существует число , отсюда имеем:

(по условию Т. 2.5.) ,

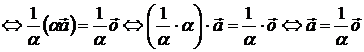(по Т. 2.5.) .

Таким образом, в случае II имеем, что .

Итак, если , то или .

Теорема 2.9. .

Доказательство:

Для того, чтобы установить, что вектор является противоположным для вектора , необходимо и достаточно проверить, выполняется ли следующее равенство: