Аксиоматика векторного пространстваРефераты >> Математика >> Аксиоматика векторного пространства
Аналогично устанавливаются остальные две формулы теоремы косинусов для треугольника.
Следствие. В треугольнике две стороны конгруэнтны тогда и только тогда, когда лежащие против них углы конгруэнтны.
Доказательство:
I. Пусть 
. Докажем, что 
.
Имеем
.
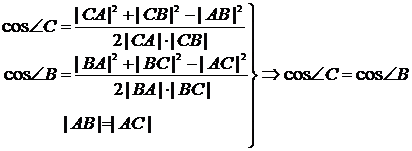II. Пусть . Докажем, что 
. Выполним следующие преобразования
– 
,
,
,
,
.
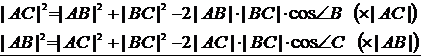Докажем, что 
; то 
;
, но для треугольника 
.
Таким образом,
.
Теорема 18.6.
, (1)
(2)
(3)
Доказательство:
Докажем равенство (1). Рассмотрим равенство: 
. Умножим его скалярно на 
:
, или так как 
, то
, или
, это и есть равенство (1).
Аналогично устанавливается остальные соотношения.
Следствие 2. Если один из углов в треугольнике тупой, то два других острые.
Доказательство:
Пусть 
– прямой, то есть 
.
Имеем:
,
.
Тогда:
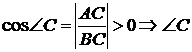– острый,
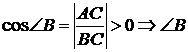– острый.
Следствие 3. В треугольнике более одного тупого угла быть не может.
Доказательство:
Пусть – тупой угол, то есть 
.
Тогда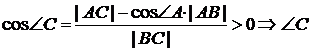 
– острый.
Аналогично устанавливается, что 
– острый.
Определение 18.6. Треугольник называется прямоугольным, если он имеет прямой угол.
Теорема 18.7. (теорема Пифагора). Если в 
– прямой, то 
.
Доказательство:
Имеем: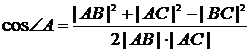 
.
Так как – прямой, то .
Тогда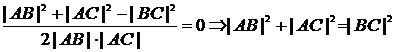 
.
Теорема 18.8. (обратная теорема 18.7). Если в , то этот треугольник прямоугольный.
Доказательство получается в результате проведения предыдущих рассуждений в обратном порядке.
Следствие 4. В прямоугольном треугольнике каждый катет меньше гипотенузы.
Доказательство:
Пусть , тогда имеем:
,
.
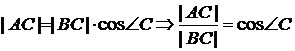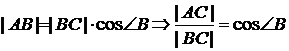Так как углы С и В острые, то 
и 
.
Отсюда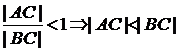 
и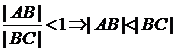 
.
§6.2. Конгруэнтность треугольников
Определение 18.7. Если треугольник АВС называется конгруэнтным треугольнику А1В1С1, если
,
.
Обозначение: 
– треугольник АВС называется конгруэнтным треугольнику А1В1С1.
Теорема 18.9. Если , то .
Доказательство:
Имеем:
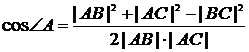, (1)
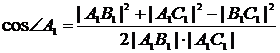(2)
По условию теоремы .
Отсюда и из равенств (1) и (2) следует, что 
, то есть 
Аналогично устанавливается и соотношения 
, 
. Отсюда .
Теорема 18.10. Если 
и
то .
Доказательство:
Скачать реферат
