Аксиоматика векторного пространства

Рефераты >> Математика >> Аксиоматика векторного пространства

На основании теоремы 18.5. имеем:

,

.

Отсюда, учитывая условия теоремы, получим , то есть .

На основании предыдущей теоремы .

Теорема 18.11. Если , и , .

Доказательство:

Если , то доказанному выше . Если , то отложим на луче [АС) от точки А отрезок [А1С1] (рис.):

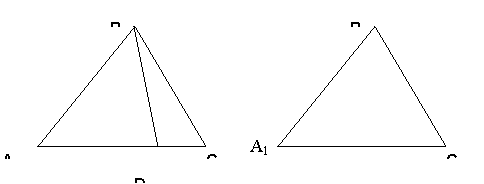. Тогда на основании предыдущей теоремы . Из конгруэнтности этих треугольников следует, что . Имеем: на луче [ВА) в полуплоскости, содержащей точку С, отложены два угла (различных) и , конгруэнтных одному и тому же углу . Последнее противоречит теореме 18.4., следовательно и .

§7. Элементы тригонометрии

§7.1. Билинейная кососимметричная функция

Определение 19.1. Если каждым двум векторам и ставится в соответствие каждое действительное число такое, что:

1) ;

2) ;

3) .

то функция называется билинейной кососимметрической функцией.

Теорема 19.1. Пусть и – произвольная база плоскости и – некоторое действительное число. Тогда существует одна и только одна кососимметрическая функция такая, что:

.

Доказательство:

Пусть в заданном базисе два произвольных вектора и имеют разложения:

Составим функцию

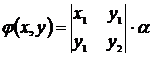(1)

Нетрудно проверить, что билинейная кососимметрическая функция, причем, если , то

.

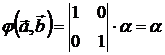Доказательства единственности. (методом от противного).

Допустим, что существует билинейная кососимметрическая функция

, такая, что .

Если – билинейная функция, то

= =

= =

= .

Учитывая, что , получим .

Аналогично . Кроме того, . Тогда

По предположению . Поэтому:

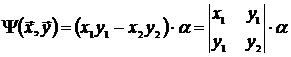(2)

Из (1) и (2) следует, что .

Примечание. Из проведенного рассуждения видно, что какое бы число мы ни взяли и какую бы мы ни взяли базу векторов и , существует единственная билинейная кососимметрическая функция такая, что .

Это обстоятельство говорит, что с помощью кососимметрической функции нельзя отличить ортонормированную базу от прочих. На этот счет требуется специальное соглашение. Договоримся, если база ортонормированная, то будем полагать .

Определение 19.2. Пусть – два произвольных единичных вектора. Значение билинейной кососимметрической функции при выбранном ортонормированном базисе , и выполнении соглашения называется синусом угла между векторами и .