Аксиоматика векторного пространства

Рефераты >> Математика >> Аксиоматика векторного пространства

, или все равно, что .

Имеем:

Таким образом или . И, следовательно, .

Рассмотренные свойства операций над векторами аналогичны соответствующим свойствам арифметических операций над числом. Так, например, сумма конечного числа векторов, как и сумма в любой коммуникативной группе, не зависит ни от порядка слагаемых в этой сумме, ни от способа расстановки скобок:

и т.д.

Однако между векторной и числовой алгеброй существуют серьезные отличия. Одно из наиболее существенных отличий состоит в том, что множество векторов не является упорядоченным, т.е. для векторов нельзя ввести отношение «меньше» и «больше». Например для двух противоположных чисел и мы знаем, что и, что одно из этих двух чисел больше 0, а другое – меньше 0. Для векторов же, удовлетворяющих равенству , постановка вопроса о том, какой из векторов или больше нулевого, а какой меньше нулевого, бессмысленна.

§3. Размерность

Определение 3.1. Векторное пространство называется n-мерным, если в нем имеется n линейно независимых векторов, а всякие n+1 векторы линейно зависимы.

Иначе говоря, размерность векторного пространства – это максимальное число содержащихся в нем линейно независимых векторов.

Если максимальное число линейно независимых векторов равно 1, то векторное пространство называется одномерным, если это число равно 2,. То векторное пространство называется двумерным, и т.д.

Векторное пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором существует сколь угодно линейно независимых векторов, называется бесконечномерным.

Определение 3.2. Совокупность n линейно независимых векторов n-мерного векторного пространства называется его базой.

Теорема 3.1. Каждый вектор n-мерного векторного пространства можно представить, и притом единственным образом, в виде линейной комбинации векторов базы.

Доказательство:

Пусть – произвольная база n-мерного векторного пространства. Так как любые n+1 векторы n-мерного векторного пространства линейно зависимы, то векторы

,

линейно зависимы, т.е. нулевой вектор является нетривиальной линейной комбинацией векторов :

,

где не все равны нулю. При этом . Если бы , то тогда среди чисел хотя бы одно было отлично от нуля, а отсюда следует, что векторы линейно зависимы.

Пусть например, , тогда .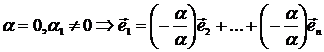

Откуда следует линейная зависимость векторов , что противоречит условию.

Итак, . Если , то

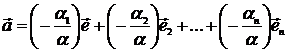
Полученное представление вектора является искомым.

Докажем, что оно единственно.

Допустим, что возможны два представления вектора в виде линейной комбинации базы:

и .

Тогда

, отсюда

.

Так как векторы линейно независимы, то

и, следовательно,

.

Ч.т.д.

Примеры.

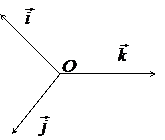1. Определим размерность векторного пространства геометрических векторов трехмерного пространства.

Докажем, что любые три вектора выходящие из одной точки О и не лежащие в одной плоскости, являются линейно независимыми, а всякие четыре вектора линейно зависимы.

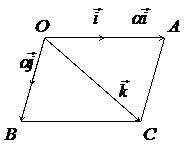В самом деле, векторы независимы, т.к. в противном случае один из них, например , должен был бы линейно выражаться через два других. Однако равенство : вектор является диагональю параллелограмма, построенного на векторах и . Отсюда векторы и и – компланарны, что противоречит условию их выбора.

Докажем теперь, что любые четыре вектора – линейно зависимы.

Возможны следующие случаи.

а) Векторы компланарны, тогда любая тройка векторов линейно зависима. Если система имеет подсистему линейно зависимых векторов, то эта система линейно зависима.