В самом деле:

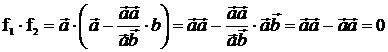
Кроме того, векторы f1 и f2 ненулевые.

7.(Теорема Пифагора). Если векторы и ортогональны, то

Доказательство:

Так как Тогда

Определение 5.4. База евклидова пространства называется ортогональной, если для всех

Если при этом еще при , то база называется ортонормированной.

8. Попарно ортогональные ненулевые векторы линейно независимы.

Доказательство:

Пусть векторы попарно ортогональны и все отличны от нулевого вектора. Рассмотрим равенство . Умножая обе части этого равенства последовательно на векторы , получим:

…………………………………………

Откуда,

Так как , то из полученных равенств следует a1=a2=…=an=0.

Это означает, что система векторов , линейно независима.

9. Существуют три ненулевых попарно ортогональных вектора.

Доказательство:

Пусть и два ненулевых ортогональных вектора, существование которых обеспечено следствием 6. Подберем ненулевой вектор такой, что и Положим , где - вектор. Образующий с векторами и в условиях следствия 6 линейно независимую систему. Тогда

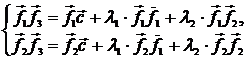
Отсюда

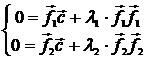
Имеем:

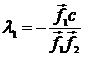и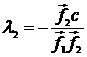

Таким образом, отправляясь от трех линейно независимых векторов и , мы построили три ненулевых вектора , которые попарно ортогональны.

Обобщение. Привлекая последовательно все базы n-мерного евклидового пространства, можно построить аналогично следующие системы ненулевых попарно ортогональных векторов:

…………

Так как система векторов линейно независима и содержит n векторов (максимальное число линейно независимых векторов), то в результате получена в n-мерном пространстве ортогональная база .

Описанный процесс известен в математике под названием процесса ортогонализации.

Имея ортогональную базу, нетрудно получить с ее помощью ортонормированную базу. Для этого вместо каждого вектора нужно взять вектор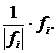

Убедимся, что длина этого вектора равна 1. В самом деле,

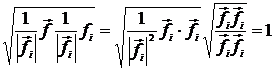
§6. Аксиоматика точечно-векторного евклидова пространства

§6.1. Метрические соотношения в треугольнике

Теорема 18.5. (теорема косинусов для треугольника).

Во всяком треугольнике

,

,

.

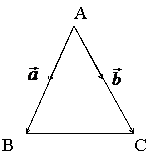
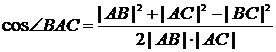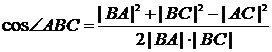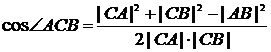Доказательство:

Рассмотрим векторное равенство . Возьмем скалярный квадрат:

,

,

.

Пусть - единичный вектор, отложенный от точка А на луче [АВ), - единичный вектор, отложенный от точки А на луче [АС). Тогда

.

Отсюда

,

.
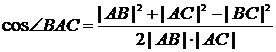