XV. Скалярное умножение диструбутивно относительно сложения векторов:

XVI. Для любого вектора и

Примеры.

1. рассмотрим трехмерное пространство геометрических векторов. Под скалярным произведением двух векторов и будем понимать число , где и длины векторов и соответственно, а a - угол между данными векторами.

Нетрудно установить, что, определив скалярное произведение таким образом, мы удовлетворим всем аксиомам скалярного произведения двух векторов. Следовательно, трехмерное пространство геометрических векторов с введенным таким образом скалярным произведением является евклидовым.

2. Рассмотрим трехмерное пространство арифметических векторов. Под скалярным произведением векторов (x1;y1;z1) и (x2;y2;z2) будем понимать число легко можно проверить, что аксиомы скалярного произведения двух векторов будут удовлетворены. Следовательно, трехмерное пространство арифметических векторов (с введенным таким образом скалярным произведением) является евклидовым.

3. Рассмотренный пример можно обобщить на n-мерное пространство арифметических векторов, если скалярное произведение двух векторов и .

Определить равенством (1)

Таким образом, n-мерное пространство арифметических векторов с введенным равенством (1) скалярным произведением, является евклидовым.

§5. Следствия из аксиом скалярного произведения

1.

Доказательство:

Имеем (1). Тогда

Определение 5.1. называется длиной вектора .

Обозначение: - длина вектора .

Таким образом, .

2. . Это вытекает из принятого определения и следствия 1.

3. , где - вектор, противоположный вектору .

Доказательство:

4. Для любых и имеет место неравенство Коши-Буняковского:

Доказательство.

Рассмотрим скалярное произведение вектора на себя.

Имеем:

(XVI)

где t – любое действительное число. Отсюда на основании аксиом XIII-XV получаем:

Выражение в левой части неравенства представляет собой квадратный трехчлен относительно t. Так как этот трехчлен должен быть неотрицательным при всех значениях t, то он не может иметь двух различных корней и, поэтому, его дискриминант:

Отсюда

Определение 5.2. Число называют косинусом угла между векторами и .

Итак,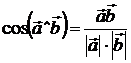

Введение такого определения оправдывается, в частности, следующими неравенствами:

Этот факт непосредственно следует из следствия 4.

5. (Неравенство треугольника)

Доказательство:

Воспользуемся неравенством Коши-Буняковского:

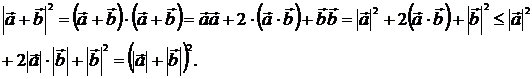
Откуда:

Определение 5.3. Векторы и называются ортогональными, если их скалярное произведение равно 0.

Обозначение: - и - ортогональные векторы.

Итак,

6. Существуют два ненулевых ортогональных вектора.

Доказательство:

Пусть даны два линейно независимых вектора и .

Рассмотрим два вектора: и .

Подберем l так, чтобы последнее равенство последовательно преобразуем так: =0 Þ

Таким образом, векторы и ортогональны.