Аксиоматика векторного пространства
Рефераты >> Математика >> Аксиоматика векторного пространства

Итак,

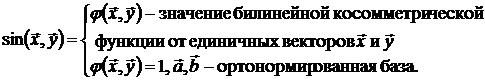
В иной форме:

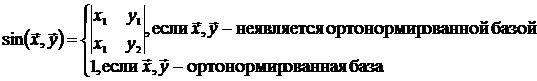
Теорема 19.2. или . На основании определения 19.2. имеем:

.

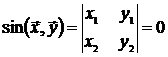Отсюда,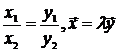. Докажем достаточность. Пусть , где .

Докажем, что .

В силу определения 19.2. имеем:

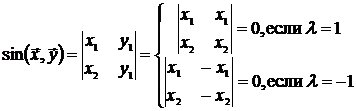
Теорема 19.3. .

Доказательство:

Пусть – единичные векторы и .

Имеем:

,

Тогда

.

§7.2. Геометрическое истолкование косинуса и синуса угла между двумя единичными векторами

В

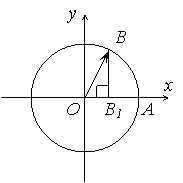На основании соотношения

Для произвольного треугольника имеем (рис.).

Так как , то

Наша окружность единичного радиуса ,

поэтому:

Таким образом, косинус угла между двумя единичными векторами и есть длина отрезка, который является проекцией отрезка [ОВ] на прямую (ОА), причем эта длина берется со знаком «+» если и со знаком «–» если .

Из соотношения имеем, что геометрически представляет собой длину катета или проекцию единичного вектора ОВ на ось у, причем в верхней полуплоскости .

§7.3. Основные соотношения между тригонометрическими функциями

Пусть и два единичных вектора.

Непосредственно из определений следует, что

,

, , если

, если

Теорема 19.4.

Доказательство:

Пусть – единичные векторы, .

Положим,

,

,

На основании определений 18.5 и 19.2. имеем:

.

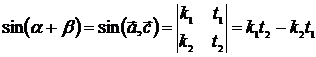Выполнив несложные преобразования, получим:

, или ,

, или ,

или ,

или .

Тогда

Следствие 19.1.

Доказательство:

Глава 2

1. Некоторые векторные равенства

Среди векторных соотношений можно выделить несколько важных соотношений, называемых здесь основными. Эти основные соотношения являются, образно выражаясь, ключами к решению широкого класса задач.

I Основное соотношение. Во всяком треугольнике ЛВС выполняется равенство

(I)

Где М – центроид (точка пересечения медиан) треугольника АВС.

Докажем соотношение (I).

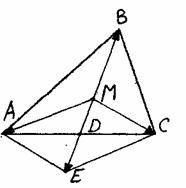Пусть М – центроид треугольника АВС. Соединим точку М со всеми вершинами треугольника. Прямая МВ пересекает сторону АС треугольника АВС в точке О, являющейся серединой стороны АС. На прямой ВМ откладываем МЕ = ВМ и соединяем точку Е с вершинами А и С. очевидно, что АМСЕ –параллелограмм. Поэтому . Откуда . Так как , то . Ч.т.д.


Страница: