Методы построения эмпирических зависимостей при обработке экспериментальных данных

Рефераты >> Статистика >> Методы построения эмпирических зависимостей при обработке экспериментальных данных

Для регрессии вида

найдем коэффициенты по формулам

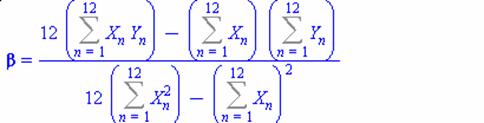
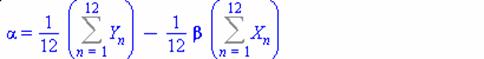
Вычислим

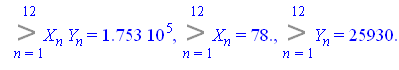
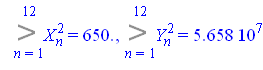
Откуда

Тогда линейная регрессия будет иметь вид

Нарисуем точки и регрессию:

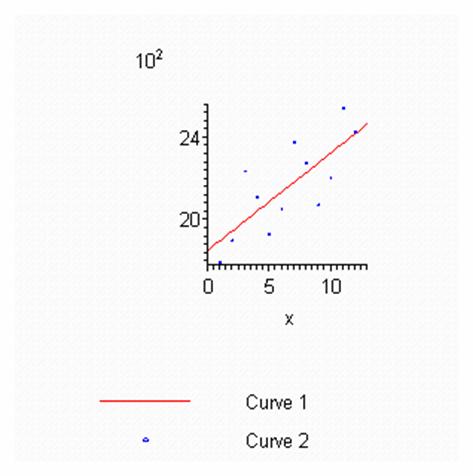
Рисунок 1. график регрессии

Найдем оценки дисперсий коэффициентов регрессии

Получим

Подсчитаем оценку дисперсии ошибки, т.е.

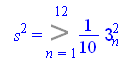
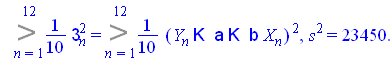
1.1.2. Эластичность

Подсчитаем эластичность по формуле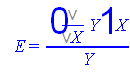

В нашем случае 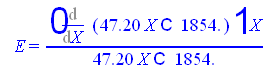или

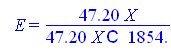
1.1.3. Доверительные интервалы для оцененных параметров

Уровень доверия . Количество степеней свободы 10. Критическое Значение статистики Стьюдента .

Доверительный интервал для beta

равен

Не можем на данном уровне значимости принять гипотезу beta=0 т.к. не попадает в доверительный интервал.

Доверительный интервал для alpha

равен

Мы не можем на данном уровне значимости принять гипотезу alpha=0 т.к. не попадает в доверительный интервал.

1.1.4. Критерий Фишера значимости всей регрессии

Коэффициент корреляции

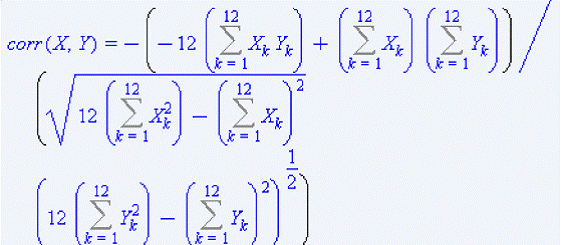
показывает, что связь средней силы

Коэффициент детерминации

показывает, что регрессия объясняет 57,93 вариации признака.

Убедимся в значимости модели с помощью статистики Фишера [1]

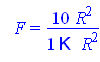
которая больше критического значения

Следовательно, регрессия значима

Проверим значимость коэффициента корреляции

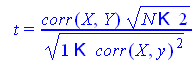
поэтому выборочный коэффициент корреляции значимо отличается от нуля.

Средняя ошибка аппроксимации

1.1.5. Изучение колеблемости и сезонности

Колеблемость - это отклонения уровней динамического ряда от тренда, т.е. остатки регрессии. Найдем остатки регрессии (т.е. очищаем признак от тренда)

Нарисуем график остатков

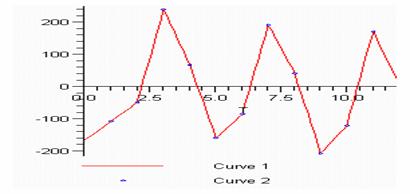
Рис. 2. Остатки

Можно видеть циклическое отклонение от тренда. Четко прослеживается сезонность ВВП. В первом квартале признак имеет наименьшее значение, а потом возрастает к третьему, а в четвертом квартале опять сокращается. Таким образом, колеблемость ВВП не является хаотической.

Рассмотрим вопрос, насколько сильно в среднем ВВП отклоняется от тренда. Для этого служит показатель среднего линейного отклонение уровней ряда от тренда

Значит в среднем, ряды уровней отклоняются от тренда на 144,8. Учтем теперь направление отклонения. Для этого будем учитывать направление отклонения, т.е. уберем модуль в предыдущей формуле: получим, что среднее отклонения равно −0.4.

Т.е. в среднем уровень ВВП находится чуть ниже трендовой траектории. За счет каких кварталов имеем этот эффект? Для этого найдем среднее арифметическое отклонений в соответствующих кварталах

Таблица 2. Средние отклонения по кварталам