Методы построения эмпирических зависимостей при обработке экспериментальных данных

Рефераты >> Статистика >> Методы построения эмпирических зависимостей при обработке экспериментальных данных

Представим их на графике

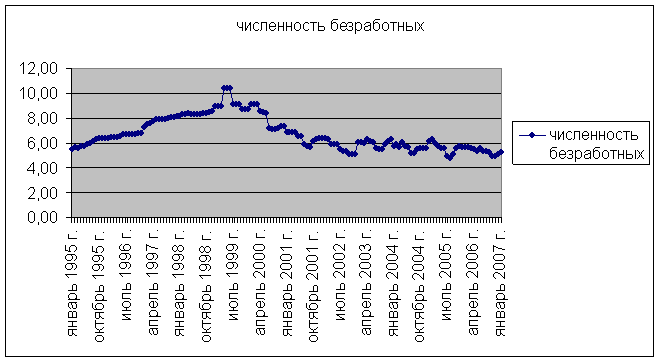
Рис 9. Динамика

можно видеть, что численность безработных росла до 99г., а потом снижалась. Это связано с оздоровлением экономики, вызванным кризисом 98г. поэтому будем изучать безработицу начиная с июня 99, когда она достигла своего максимума. На этом временном интервале она представима на графике

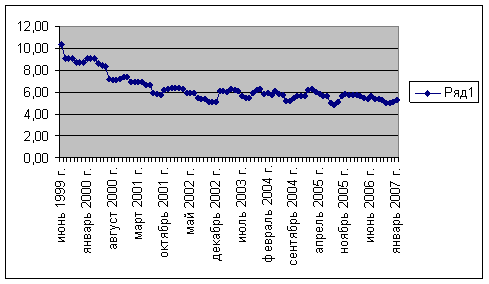
Рис 10. Динамика ряда за 1999-2007гг.

построим регрессию количества безработных по времени

2.1. Построение регрессии

Для регрессии вида

найдем коэффициенты по формулам

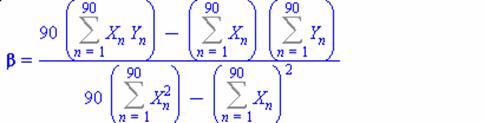
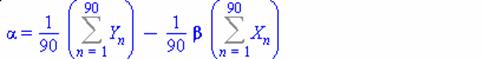
Тогда

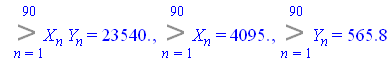
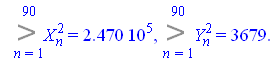
Откуда

Тогда линейная регрессия будет иметь вид

Смысл коэффициента β заключается в том, что при изменении значения X на 1 единицу Y меняется на -0, 03626 единиц.

Нарисуем точки и регрессию:

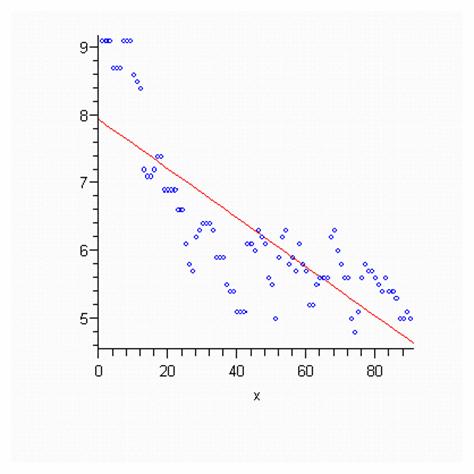
Рис 11. График регрессии

2.2. Дисперсионный анализ

Среднее Y

Остаточная вариация (RSS)

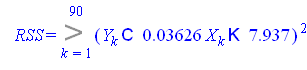
Общая вариация (TSS)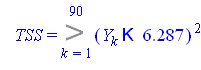

Объясняемая вариация (ESS)

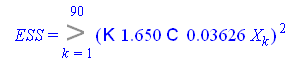
Правило сложения дисперсий выполняется

Найдем оценки дисперсий коэффициентов регрессии

по формулам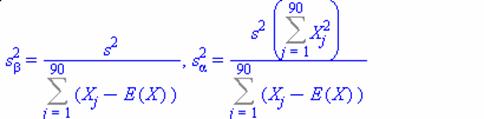

Получим

Подсчитаем оценку дисперсии ошибки, т.е.

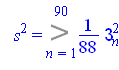
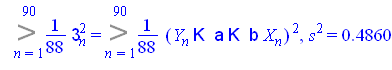
2.3. Эластичность

Подсчитаем функцию эластичности по формуле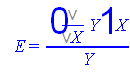

В нашем случае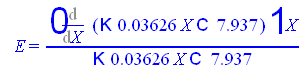

Или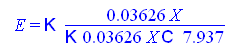

Значение эластичности в средней точке

Показывает, что при изменении X на 1% Y меняется на -0,2624 процентов.

2.4. Изучение качества регрессии

2.4.1. Доверительные интервалы для оцененных параметров

уровень доверия

Количество степеней свободы 88

Критическое значение статистики Стьюдента

Доверительный интервал для beta

равен [ -0,042750869; -0,031196821]

Не можем на данном уровне значимости принять гипотезу beta=0 т.к. не попадает в доверительный интервал.

Доверительный интервал для alpha

равен [7,741799269; 8,360507467 ]

Мы не можем на данном уровне значимости принять гипотезу alpha=0 т.к. не попадает в доверительный интервал.

2.4.2. Критерий Фишера значимости всей регрессии

Коэффициент корреляции

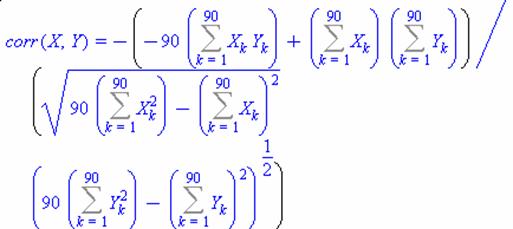
показывает, что связь сильна и отрицательна

Коэффициент детерминации

показывает, что регрессия объясняет 65, 22 процентов вариации признака.

Убедимся в значимости модели с помощью статистики Фишера

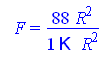
которая больше критического значения

Следовательно, регрессия значима

Проверим значимость коэффициента корреляции

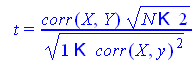
поэтому выборочный коэффициент корреляции значимо отличается от нуля.

Средняя ошибка аппроксимации

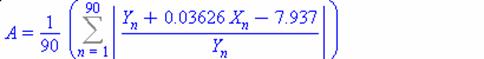
2.5. Колеблемость признака

Найдем остатки регрессии (т.е. очищаем признак от тренда)