Вода

Рефераты >> Физика >> Вода

На основании данных для авторами была рассчитана изотермическая сжимаемость из соотношения

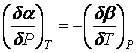
и теплоемкость СР из соотношения

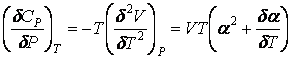
Полученные результаты привели авторов к выводу, что при Т = - 45°С и давлении Р = 1 атм должна иметь место -точка для перечисленных выше величин.

Аналогичная зависимость для статической диэлектрической постоянной и электропроводности была получена Ангелом и др.(1978).

Общая формула для описания поведения функции в окрестности -точки может быть записана в виде

,

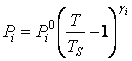где - изучаемый параметр, = 228 К; и - коэффициенты. По данным Ангела, увеличивается от 85 при 0°С до 107 при -35°С, а (ом-1·см-1) изменяется от –4,4 при 0°С до –5 при 35°С, т.е. уменьшается с уменьшением температуры от 0°С до -35°С.

IV СТАТИЧЕСКАЯ ДИЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ

Диэлектрическая постоянная вещества зависит от поляризуемости частиц, входящих в состав диэлектрика, от их числа в единице объема и от их взаимного расположения и, следовательно, представляет собой довольно сложную структурную характеристику вещества.

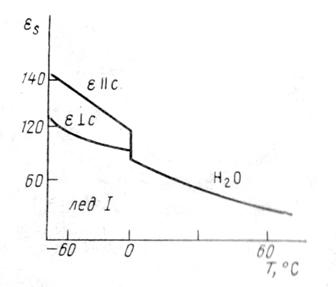Статическая диэлектрическая постоянная в анизотропной среде, каковой является лед I, представляет собой тензор и характеризуется двумя компонентами: ε2 и εz, где ε2 - компонента ε в направлении, параллельном оси С кристалла льда Ih, εz - компонента в направлении, перпендикулярном оси С. В жидкой воде не зависит от направления, и ее значение при T = 0°C несколько меньше, чем величина εz во льду I (рис.13).

Так как плотность воды больше, чем плотность льда I, то можно было бы ожидать, что в воде будет больше, чем во льду I. То, что это не так, свидетельствует в пользу того, что при плавлении изменяются или две другие переменные, или какая-то одна из них, от которых зависит , а именно поляризуемость определяющих частиц и их взаимное расположение. Уменьшение при плавлении и последующее уменьшение при нагревании Попл (1951) объясняет изгибанием водородных связей (1.12). Наибольшее изгибание связей имеет место при плавлении. По Поплу, среднее отклонение от угла водородной связи при 0°С составляет ~26°С и растет с ростом температуры. В своем расчете статической диэлектрической постоянной Попл пользуется формулой Кирквуда (1939).

В основу этой формулы была положена модель четырехсвязанной молекулы воды с экспериментальными углами между связями. Допускалось свободное вращение молекулы водорода вокруг ОН связи. Для было получено следующее выражение

,

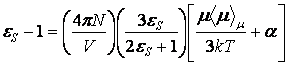где N – число Авогадро; V – объем, занимаемый грамм-молекулой воды; - дипольный момент фиксированной молекулы в произвольной сферической области диэлектрика; - средний дипольный момент выбранной произвольно сферической области диэлектрика при фиксированном , - поляризуемость;

,

где Z – число ближайших соседей; характеризует средний угол между молекулами-диполями:

,

и - относительные ориентации при вращении ближайших соседей. Согласно Фрелиху (1960),

,

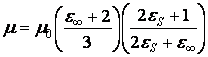где - дипльный момент молекулы воды в вакууме; .

Оценку Попл провел в предположении изгибания водородных связей. Его оценка показала, что в его модели всеми соседями, кроме четырех первых, можно пренебречь. Значение g, учитывающее взаимодействие только с четырьмя первыми соседями, у него имеет следующий вид:

,

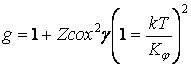где - постоянная изгибания водородных связей:

;

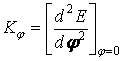Е – энергия изгибания водородных связей, определяемая как , где и - углы изгибания водородных связей. и Z Попл оценивает из радиальной функции распределения = 3,78∙10-13эрг∙рад-2. Величина g уменьшается как с ростом Т, так и с ростом давления. Так, при Т = 0ºС g = 2,91, а при Т = 70ºС g = 2,68.

Проведенный расчет привел автора к правильной температурной зависимости , которую определил рост угла изгибания водородных связей с ростом температуры. Однако абсолютные значения разошлись с экспериментальным данными, они оказались на 20% меньше.