Запишем

V∙ K(1←0) ∙∙ = p.

совместно с K(1←0) = K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) и получим:

V∙ K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) ∙∙ = p.

Эту систему линейных алгебраических уравнений можно представить в виде:

[ V∙ K(1←x2) ] ∙ { K(x2←x1) ∙ K(x1←0) ∙∙ } = p.

[ матрица ] ∙ { вектор } = вектор

Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

[ V∙ K(1←x2) ] ∙ { K(x2←x1) ∙ K(x1←0) ∙∙ } = p.

И так далее.

В итоге поочередного вычленений матриц слева из вектора и ортонормирования получим систему:

D∙ = p,

Отсюда получаем, что:

c = D2∙ (p- D1∙ u)

Таким образом, искомые константы найдены.

11. Применяемые формулы ортонормирования.

Эти формулы обсчитаны в кандидатской диссертации.

Взято из: Березин И.С., Жидков Н.П. Методы вычислений, том II, Государственное издательство физико-математической литературы, Москва, 1962 г. 635 стр.

Пусть дана система линейных алгебраических уравнений порядка n:

А=.

Здесь над векторами поставим черточки вместо их обозначения жирным шрифтом.

Будем рассматривать строки матрицы А системы как векторы:

=(,,…,).

Ортонормируем эту систему векторов.

Первое уравнение системы А=делим на .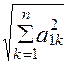

При этом получим:

++…+=, =(,,…,),

где =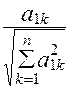, =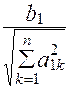, 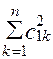=1.

Второе уравнение системы заменяется на:

++…+=, =(,,…,),

где =, =,

=-(,), =-(,).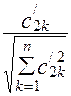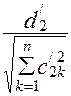