Краевые задачи. Методы решения А.Ю.Виноградова. Включая жесткие краевые задачи

Рефераты >> Математика >> Краевые задачи. Методы решения А.Ю.Виноградова. Включая жесткие краевые задачи

Аналогично поступаем дальше. Уравнение с номером i примет вид:

++…+=, =(,,…,),

где =, =,

=-(,)-(,)-…-(,),

=-(,)-(,)-…-(,).

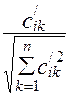Процесс будет осуществим, если система линейных алгебраических уравнений линейно независима.

В результате мы придем к новой системе С=, где матрица С будет с ортонормированными строками, то есть обладает свойством С*С= E, где Е – это единичная матрица.

(Таким образом, решение системы можно записать в виде = С.)

12. Вывод формул, позаимствованный из «Теории матриц» Гантмахера.

Система линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами имеет вид:

Y(x) = A Y(x) + F(x). (1)

Разложим Y(x) в ряд Маклорена по степеням x:

Y(x)=Y+ Yx + Yx/2! + …, где Y=Y(0), Y= Y(0), … (2).

Из (1) почленным дифференцированием при А=const и F(x)=0 получим:

Y= AY= AY, Y= A Y= AY, (3)

Положив в (3) x=0 и подставив в (2) получим:

Y(x) = Y+ Ax Y+ Ax/2! Y+ … = eY, (4)

где e= E + Ax + Ax/2! + …, где Е – единичная матрица. (5)

Если принять x=x, то (4) заменится на

Y(x) = eY(x), (6)

Рассмотрим случай A=const и F≠0.

Введем в рассмотрение вектор-функцию Ya(x) в виде: Y(x)= eYa(x). (7)

Продиффренцируем (7) и подставим в (1). Получим:

eYa(x) = F(x). (8)