for(int i=0;i<4;i++){

for(int j=0;j<8;j++){

MATRIX_many[i][j]=U[i][j];

MATRIX_many[8*11-4+i][8*11-8+j]=V[i][j];

}

B_many[i]=u_[i];

B_many[8*11-4+i]=v_[i];

}

for(int kk=0;kk<(11-1);kk++){//(11-1) единичных матриц и матриц EXPO надо записать в MATRIX_many

for(int i=0;i<8;i++){

MATRIX_many[i+4+kk*8][i+kk*8]=1.0;//заполнение единичными матрицами

for(int j=0;j<8;j++){

MATRIX_many[i+4+kk*8][j+8+kk*8]=-expo_from_minus_step[i][j];//заполнение матричными экспонентами

}

}

}

//Решение систем линейных алгебраических уравнений

GAUSS(MATRIX_many,B_many,Y_many);

//Вычисление векторов состояния в 101 точке - левая точка 0 и правая точка 100

exponent(A,step,expo_from_plus_step);

for(int i=0;i<11;i++){//заполнение промежуточных точек во всех 10-ти интервалах (всего получим точки от 0 до 100) между 11 узлами

for(int j=0;j<8;j++){

Y[0+i*10][j]=Y_many[j+i*8];//в 11-ти узлах векторы беруться из решения СЛАУ - из Y_many

}

}

for(int i=0;i<10;i++){//заполнение промежуточных точек в 10-ти интервалах

for(int j=0;j<8;j++){

Y_vspom[j]=Y[0+i*10][j];//начальный вектор для i-го участка, нулевая точка, точка старта i-го участка

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+1][j]=Y_rezult[j];//заполнение 1-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+2][j]=Y_rezult[j];//заполнение 2-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+3][j]=Y_rezult[j];//заполнение 3-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+4][j]=Y_rezult[j];//заполнение 4-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+5][j]=Y_rezult[j];//заполнение 5-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+6][j]=Y_rezult[j];//заполнение 6-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+7][j]=Y_rezult[j];//заполнение 7-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+8][j]=Y_rezult[j];//заполнение 8-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

mat_on_vect(expo_from_plus_step, Y_vspom, Y_rezult);

for(int j=0;j<8;j++){

Y[0+i*10+9][j]=Y_rezult[j];//заполнение 9-ой точки интервала

Y_vspom[j]=Y_rezult[j];//для следующего шага

}

}

//Вычисление момента во всех точках между краями

for(int ii=0;ii<=100;ii++){

Moment[ii]+=Y[ii][4]*(-nju*nn2)+Y[ii][6]*1.0;//Момент M1 в точке [ii]

//U[2][4]=-nju*nn2; U[2][6]=1.0; u_[2]=0;//Момент M1

}

}//ЦИКЛ ПО ГАРМОНИКАМ ЗДЕСЬ ЗАКАНЧИВАЕТСЯ

for(int ii=0;ii<=100;ii++){

fprintf(fp,"%f\n",Moment[ii]);

}

fclose(fp);

printf( "PRESS any key to continue .\n" );

_getch();

return 0;

}

21. 19 декабря 2012: Случай переменных коэффициентов (ошибка).

Где-то 2 года назад мой отец доктор физико-математических наук профессор МГТУ им. Баумана показал мне его статью в «Докладах Российской Академии наук» о том, как вычислять матрицу Коши в случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами .

До статьи моего отца это можно было делать так:

Из теории матриц [Гантмахер] известно свойство перемножаемости матричных экспонент (матриц Коши):

.

В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами , решение задачи Коши предлагается искать при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:

,

где матрицы Коши приближенно вычисляются по формуле:

, где .

Новый материал (ошибка):

Когда я читал статью своего отца, то я не понял сложный вывод формулы. А сегодня утром мне вдруг (непонятно откуда) отчётливо пришла в голову мысль о том, как можно вывести формулу моего отца почти в одно действие.

пусть

.

17 июля 2013: Исправление ошибок.

В журнале «Математическое моделирование» РАН мне сообщили, что оказывается широко известно, что для матриц А и В: exp(A+B) НЕ РАВНО exp(A)*exp(B).

1) Это означает, что ФОРМУЛА

НЕ ВЕРНА.

2) Также это означает, что следующая ФОРМУЛА ТОЖЕ НЕ ВЕРНА:

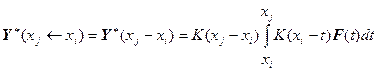
Но я даже сейчас не очень понимаю, зачем я переусложнял жизнь, когда, по-видимому, можно для участка пользоваться формулой из «Теории матриц» Гантмахера:

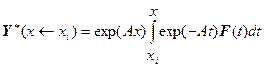, где вместо x наверное надо просто подставить .