Краевые задачи. Методы решения А.Ю.Виноградова. Включая жесткие краевые задачи

Рефераты >> Математика >> Краевые задачи. Методы решения А.Ю.Виноградова. Включая жесткие краевые задачи

И так в точку xпереносим матричное краевое условие с левого края и таким же образом переносим матричное краевое условие с правого края и получаем:

U∙ Y(x) = u ,

V∙ Y(x) = v .

Из этих двух матричных уравнений с прямоугольными горизонтальными матрицами коэффициентов очевидно получаем одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов:

∙ Y(x) = .

А в случае «жестких» дифференциальных уравнений предлагается применять построчное ортонормирование матричных краевых условий в процессе их переноса в рассматриваемую точку. Для этого формулы ортонормирования систем линейных алгебраических уравнений можно взять в [Березин, Жидков].

То есть, получив

U∙ Y(x) = u,

применяем к этой группе линейных алгебраических уравнений построчное ортонормирование и получаем эквивалентное матричное краевое условие:

U∙ Y(x) = u.

И теперь уже в это проортонормированное построчно уравнение подставляем

Y(x) = K(x←x) ∙ Y(x) + Y*(x←x) .

И получаем

U∙ [ K(x←x) ∙ Y(x) + Y*(x←x) ] = u ,

[ U∙ K(x←x) ] ∙ Y(x) = u- U∙ Y*(x←x) ,

Или получаем краевые условия, перенесенные в точку x:

U∙ Y(x) = u ,

где U= [ U∙ K(x←x) ] и u= u- U∙ Y*(x←x) .

Теперь уже к этой группе линейных алгебраических уравнений применяем построчное ортонормирование и получаем эквивалентное матричное краевое условие:

U∙ Y(x) = u.

И так далее.

И аналогично поступаем с промежуточными матричными краевыми условиями, переносимыми с правого края в рассматриваемую точку.

В итоге получаем систему линейных алгебраических уравнений с квадратной матрицей коэффициентов, состоящую из двух независимо друг от друга поэтапно проортонормированных матричных краевых условий. Эта система решается методом Гаусса с выделением главного элемента для получения решения Y(x) в рассматриваемой точке x:

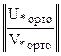∙ Y(x) = .

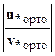4.2. Программа на С++ расчета цилиндрической оболочки.

В качестве проверочных задач использовалась схема консольно закрепленных цилиндрической и сферической оболочек с параметрами R/h=50, 100, 200. Длина цилиндрической оболочки рассматривалась L/R=2, а угловые координаты сферической оболочки рассматривались от p/4 до 3p/4. На свободном крае рассматривалось нормальное к поверхности оболочек погонное усилие, равномерно распределенное в интервале [-p/4, p/4]. В качестве среды программирования использовалась система Microsoft Visual Studio 2010 (Visual C++).